Difference between revisions of "Topographic Anisotropy"

From UMaine SECS Numerical Modeling Laboratory
Jump to: navigation, search
 
(28 intermediate revisions by 4 users not shown)
Line 1: Line 1:
−
'''Multi-scale characterization of topographic anisotropy'''
+
<h2 id="mp-itn-h2" style="margin:0.5em; width:80em; background:#cedff2; font-family:inherit; font-size:110%; font-weight:normal; border:1px solid #a3b0bf; color:#000; padding:0.2em 0.4em;">
 +
==Multi-scale characterization of topographic anisotropy==
 +
 
 +
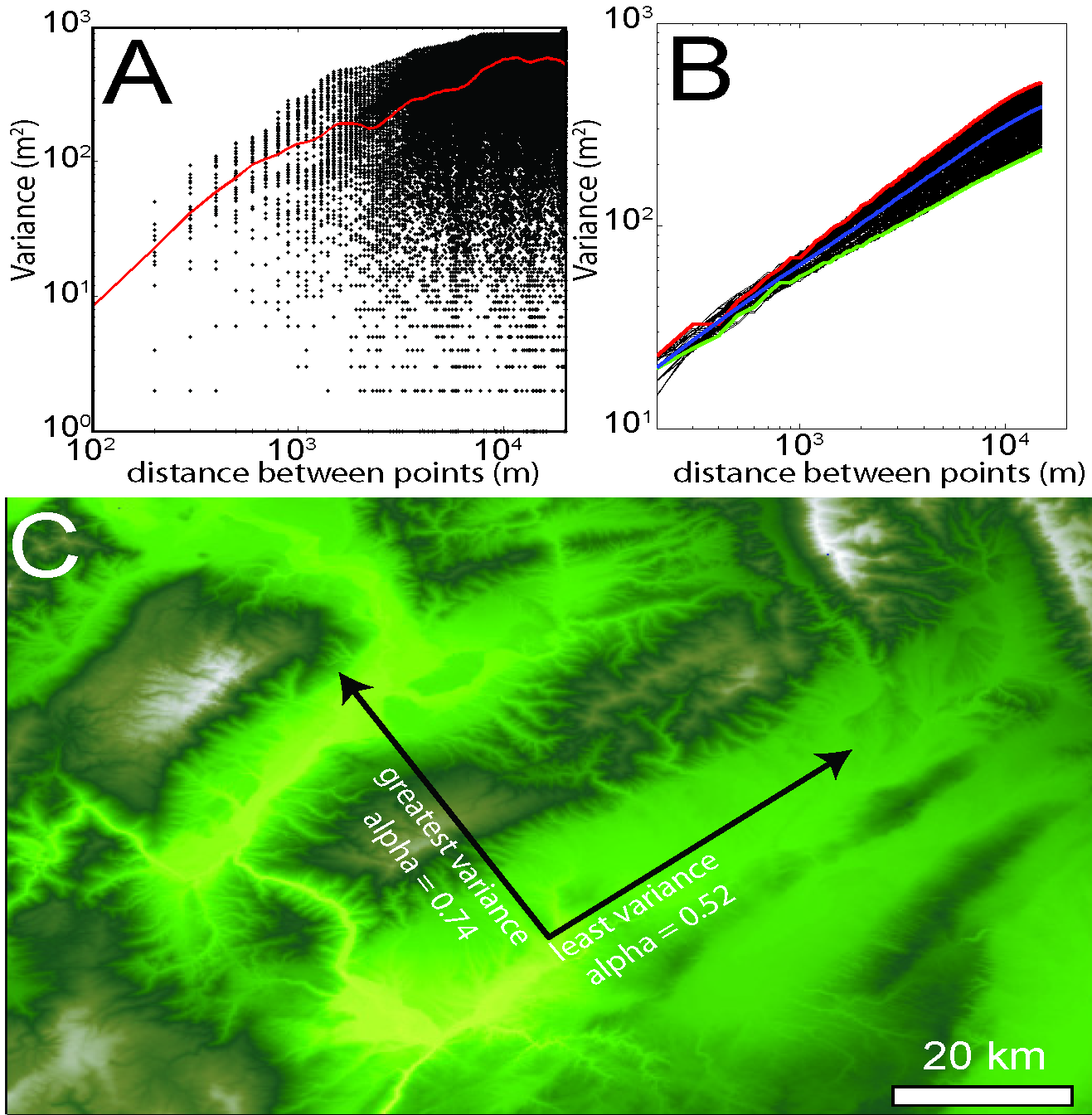
'''Abstract:''' We present a method for quantifying orientation and scale dependence of topographic anisotropy to aid in differentiation of the fluvial and tectonic contributions to surface evolution. Using multi-directional variogram statistics to track the spatial persistence of elevation values across a landscape, we calculate anisotropy as a multiscale, direction-sensitive variance in elevation between two points on a surface. Tectonically derived topographic anisotropy is associated with the three-dimensional kinematic field, which contributes 1) differential surface displacement and 2) crustal weakening along shear zones, both of which amplify processes of surface erosion. Based on our analysis, tectonic displacements dominate the topographic field at the scale of mountain ranges, while a combination of the local displacement and strength fields are well represented at the ridge and valley scale. Drainage network patterns tend to reflect the geometry of underlying active or inactive tectonic structures due to the rapid erosion of faults and differential displacement across the fault. The persistence and complexity of correlated anisotropic signals depends on how the strain field evolves with time: new tectonic regimes can overprint the original topographic signal, or the signal can slowly recede as tectonism halts. Regions that have been largely devoid of strain, such as passive coastal margins, have predominantly isotropic topography with typically dendritic drainage network patterns. These methods can be used successfully to infer the settings of past or present tectonic regimes, and can be particularly useful in predicting the location and orientation of structural features that would otherwise be impossible to interpret in the field.
 +
</h2>
 +
 
 +
 
 +
<h4 id="mp-itn-h4" style="margin:0.1em; background:#ffffff; border:1px solid #a3b0bf; color:#000; padding:0.1em 0.2em;">
 +
<gallery widths=175px heights=175px mode=packed-hover>
 +
Image:Vario figures copy Page 01.png|''[[Topographic Anisotropy Figure 1|'''Figure 1''']]''|link=[[Topographic Anisotropy Figure 1]]
 +
Image:Vario figures copy Page 02.png|''[[Topographic Anisotropy Figure 2|'''Figure 2''']]''|link=[[Topographic Anisotropy Figure 2]]
 +
Image:Vario figures copy Page 03.png|''[[Topographic Anisotropy Figure 3|'''Figure 3''']]''|link=[[Topographic Anisotropy Figure 3]]
 +
Image:Vario figures copy Page 04.png|''[[Topographic Anisotropy Figure 4|'''Figure 4''']]''|link=[[Topographic Anisotropy Figure 4]]
 +
Image:Vario figures copy Page 05.png|''[[Topographic Anisotropy Figure 5|'''Figure 5''']]''|link=[[Topographic Anisotropy Figure 5]]
 +
Image:Vario figures copy Page 06.png|''[[Topographic Anisotropy Figure 6|'''Figure 6''']]''|link=[[Topographic Anisotropy Figure 6]]
 +
Image:Vario figures copy Page 07.png|''[[Topographic Anisotropy Figure 7|'''Figure 7''']]''|link=[[Topographic Anisotropy Figure 7]]
 +
Image:Vario figures copy Page 08.png|''[[Topographic Anisotropy Figure 8|'''Figure 8''']]''|link=[[Topographic Anisotropy Figure 8]]
 +
Image:Vario figures copy Page 09.png|''[[Topographic Anisotropy Figure 9|'''Figure 9''']]''|link=[[Topographic Anisotropy Figure 9]]
 +
Image:Vario figures copy Page 10.png|''[[Topographic Anisotropy Figure 10|'''Figure 10''']]''|link=[[Topographic Anisotropy Figure 10]]
 +
</gallery>
 +
</h4>
 +
 
  
−
S.G. Roy (a), P.O. Koons (a), B. Osti (a), P. Upton (b), G.E. Tucker (c)
 
  
−
a ''Earth and Climate Sciences, University of Maine, 111 Bryand Global Sci. Ctr., Orono ME 04469''
+
{| border="1" style="border-collapse:collapse"
 +
| {{#ev:youtube|gkpHdrtumgw}}
 +
| {{#ev:youtube|e86ZIqox_Fk}}
 +
|}
  
−
b ''GNS Science, PO Box 30368, Lower Hutt 5040, New Zealand''
 
  
−
c ''Cooperative Institute for Research in Environmental Sciences (CIRES) and Department of Geological Sciences, University of Colorado, UCB 399 Boulder, CO 80309-0399''
 
  
−
'''Abstract'''
+
S.G. Roy (a), P.O. Koons (a), B. Osti (a), P. Upton (b), G.E. Tucker (c)
  
−
We present a method for quantifying orientation and scale dependence of topographic anisotropy to aid in differentiation of the fluvial and tectonic contributions to surface evolution. Using multi-directional variogram statistics to track the spatial persistence of elevation values across a landscape, we calculate anisotropy as a multiscale, direction-sensitive variance in elevation between two points on a surface. Tectonically derived topographic anisotropy is associated with the three-dimensional kinematic field, which contributes 1) differential surface displacement and 2) crustal weakening along shear zones, both of which amplify processes of surface erosion. Based on our analysis, tectonic displacements dominate the topographic field at the scale of mountain ranges, while a combination of the local displacement and strength fields are well represented at the ridge and valley scale. Drainage network patterns tend to reflect the geometry of underlying active or inactive tectonic structures due to the rapid erosion of faults and differential displacement across the fault. The persistence and complexity of correlated anisotropic signals depends on how the strain field evolves with time: new tectonic regimes can overprint the original topographic signal, or the signal can slowly recede as tectonism halts. Regions that have been largely devoid of strain, such as passive coastal margins, have predominantly isotropic topography with typically dendritic drainage network patterns. These methods can be used successfully to infer the settings of past or present tectonic regimes, and can be particularly useful in predicting the location and orientation of structural features that would otherwise be impossible to interpret in the field.
+
: a ''Earth and Climate Sciences, University of Maine''
  
−
<gallery>
+
: b ''GNS Science''
−
Image:Vario figures copy Page 01.png|''[[Topographic Anisotropy Figure 1|'''Figure 1''']]'': A) An example grid in which we apply our variance algorithm. Starting at with separation distance equal to the grid resolution...[[Topographic Anisotropy Figure 1|'''read more''']]
+
 
−
Image:Vario figures copy Page 02.png|''[[Topographic Anisotropy Figure 2|'''Figure 2''']]'': Flow chart for the EVA algorithm.
+
: c ''Cooperative Institute for Research in Environmental Sciences (CIRES) and Department of Geological Sciences, University of Colorado''
−
Image:Vario figures copy Page 10.png|''[[Topographic Anisotropy Figure 10|'''Figure 10''']]'': A) variance measured at single, randomly chosen point along 1 degree intervals for 360 degrees up to 20 km separation...[[Topographic Anisotropy Figure 10|'''read more''']]
+
 
−
</gallery>
+
[http://www.nsf.gov/awardsearch/showAward?AWD_ID=1027809 NSF-CDI-1027809]

Latest revision as of 14:09, 13 April 2018

Multi-scale characterization of topographic anisotropy

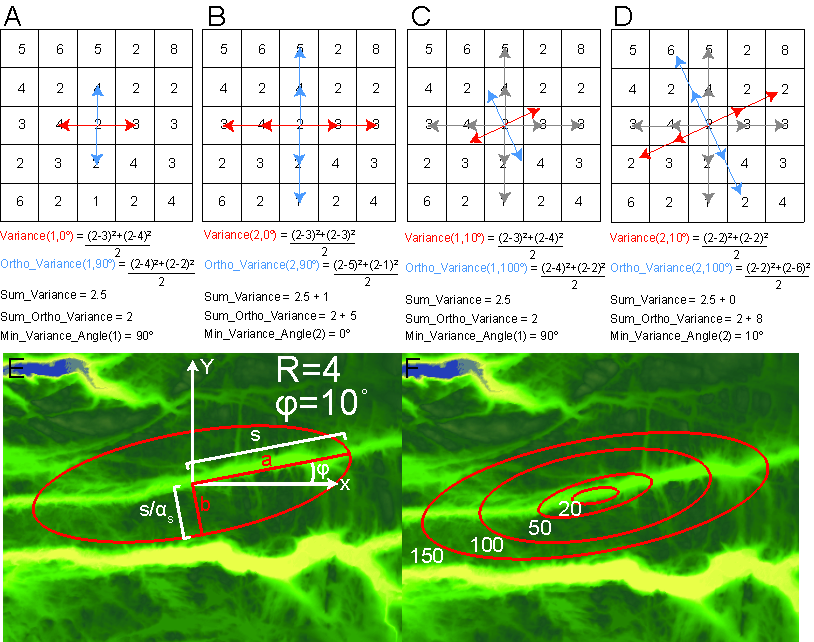
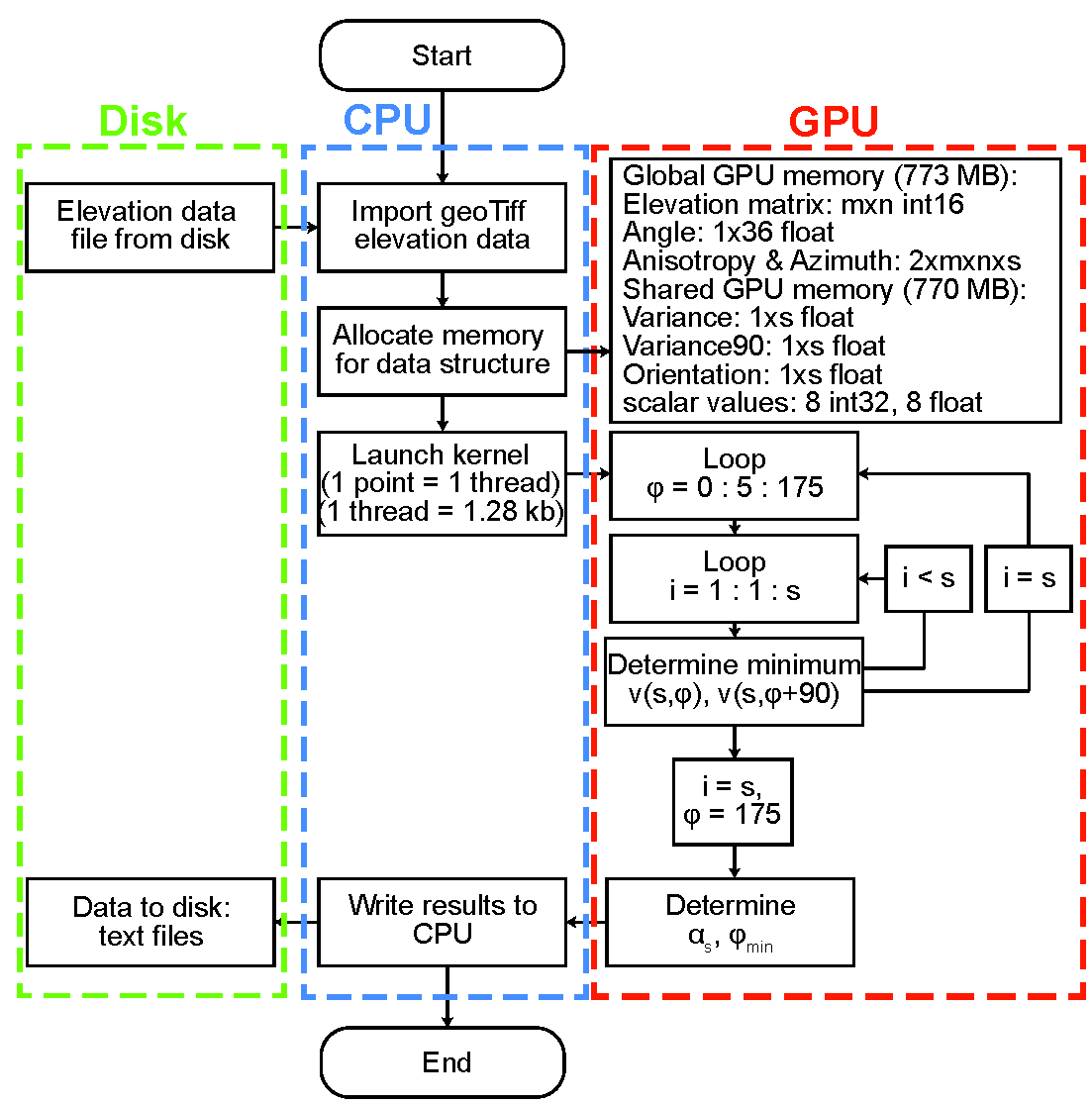
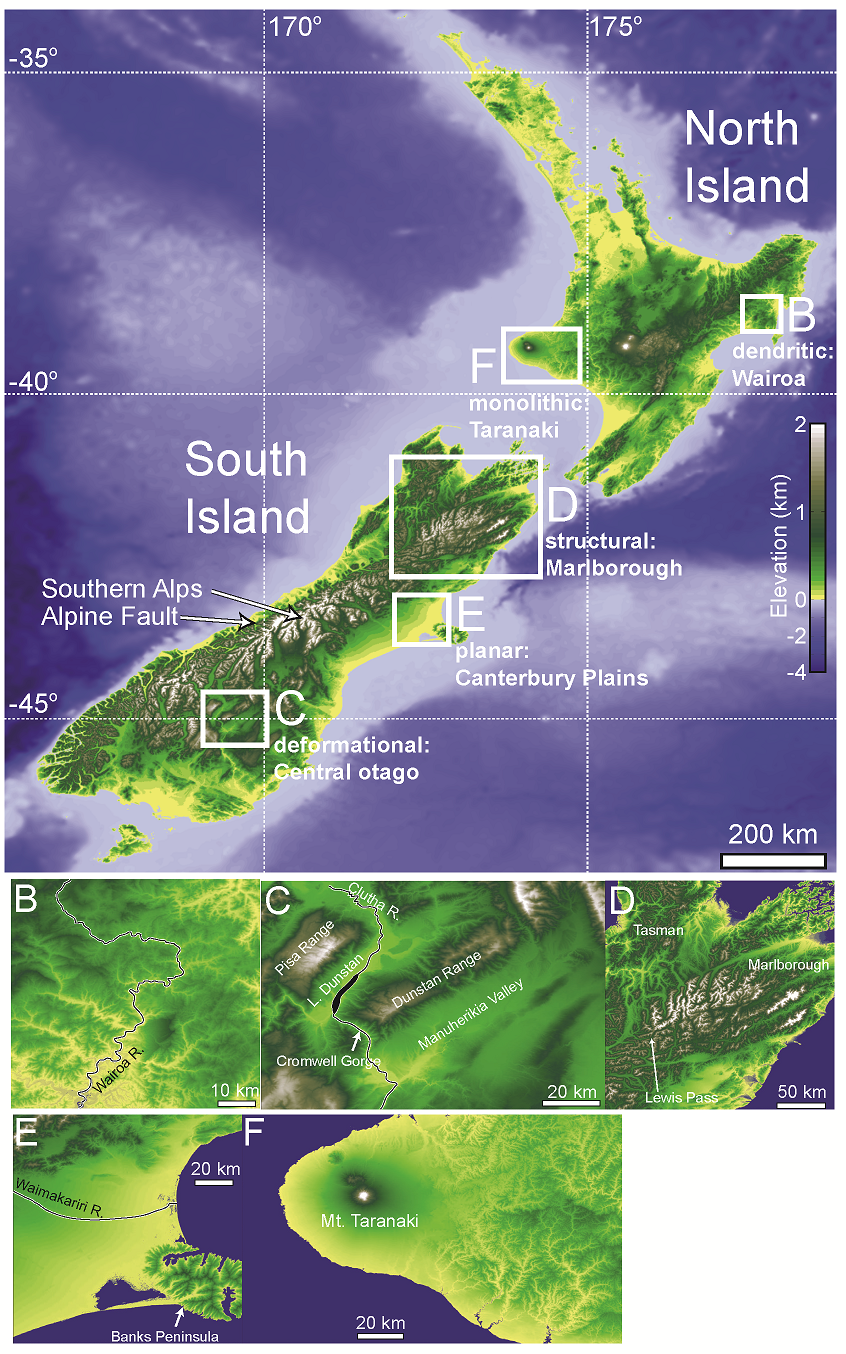
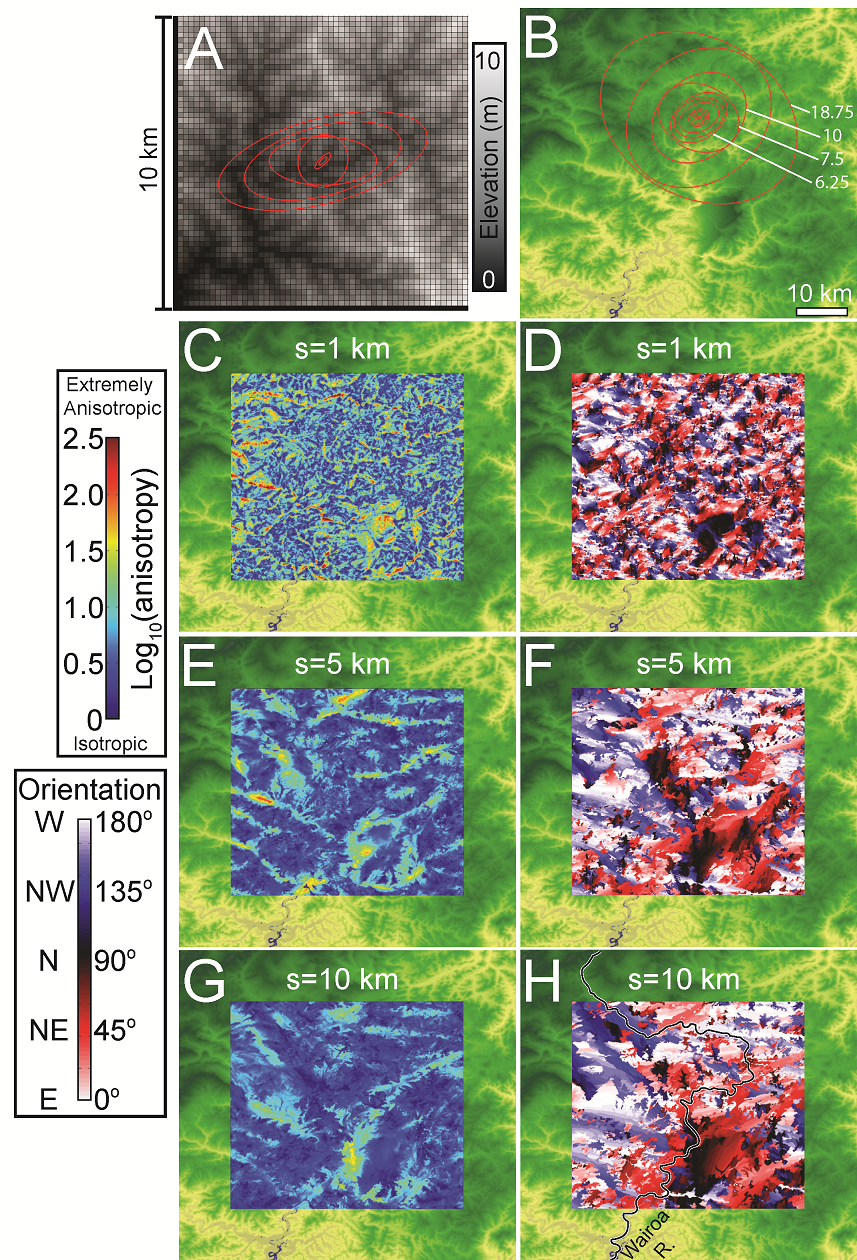
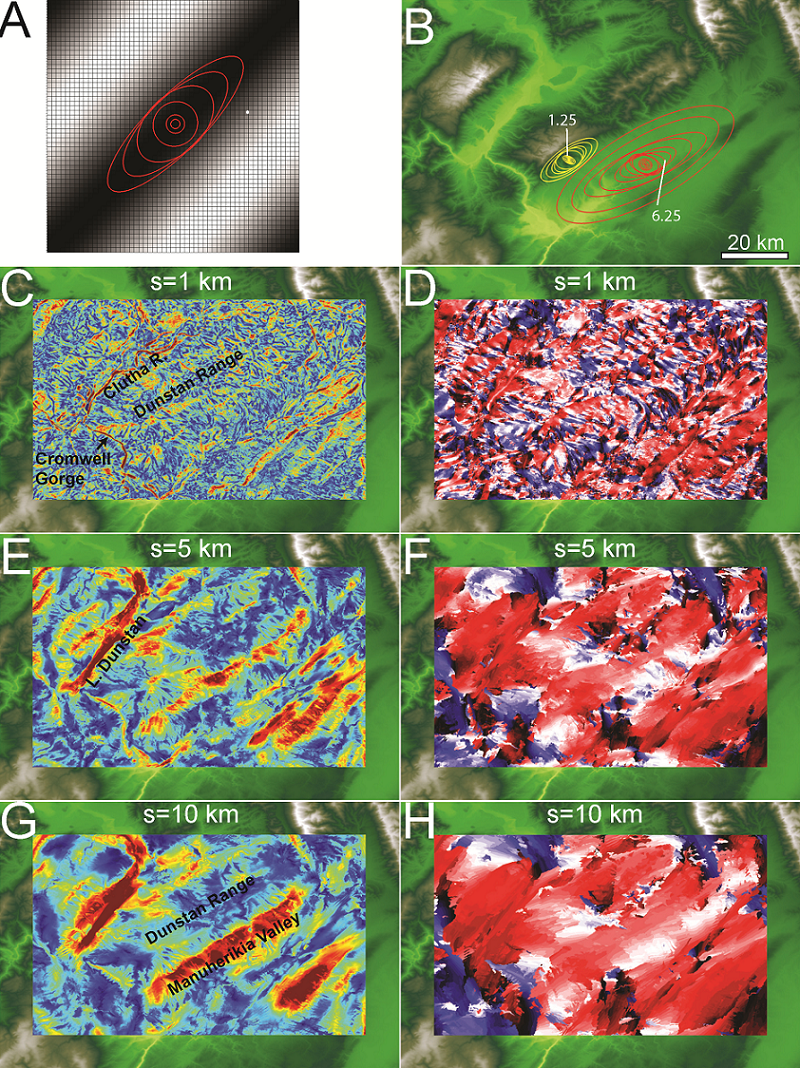
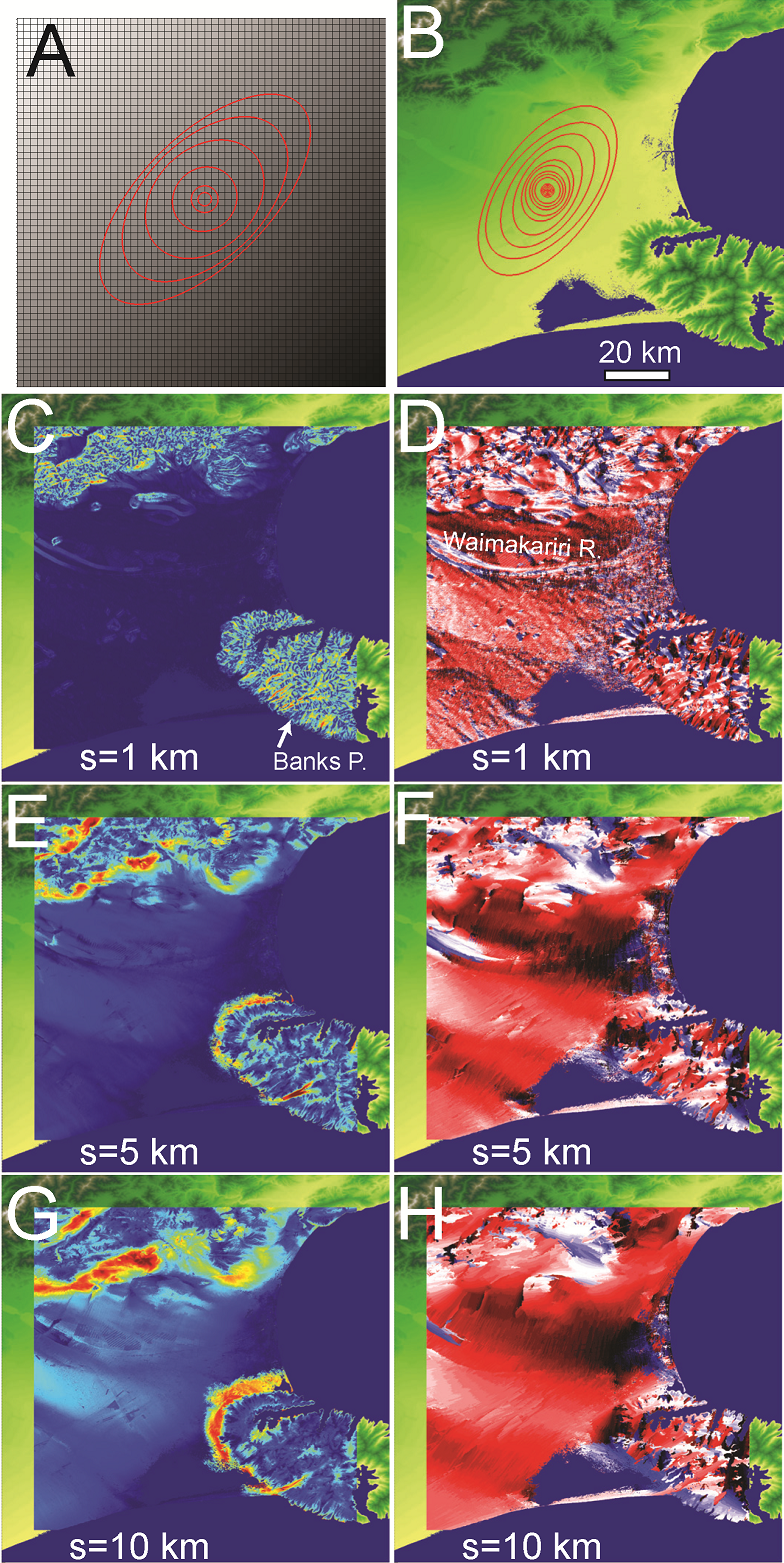
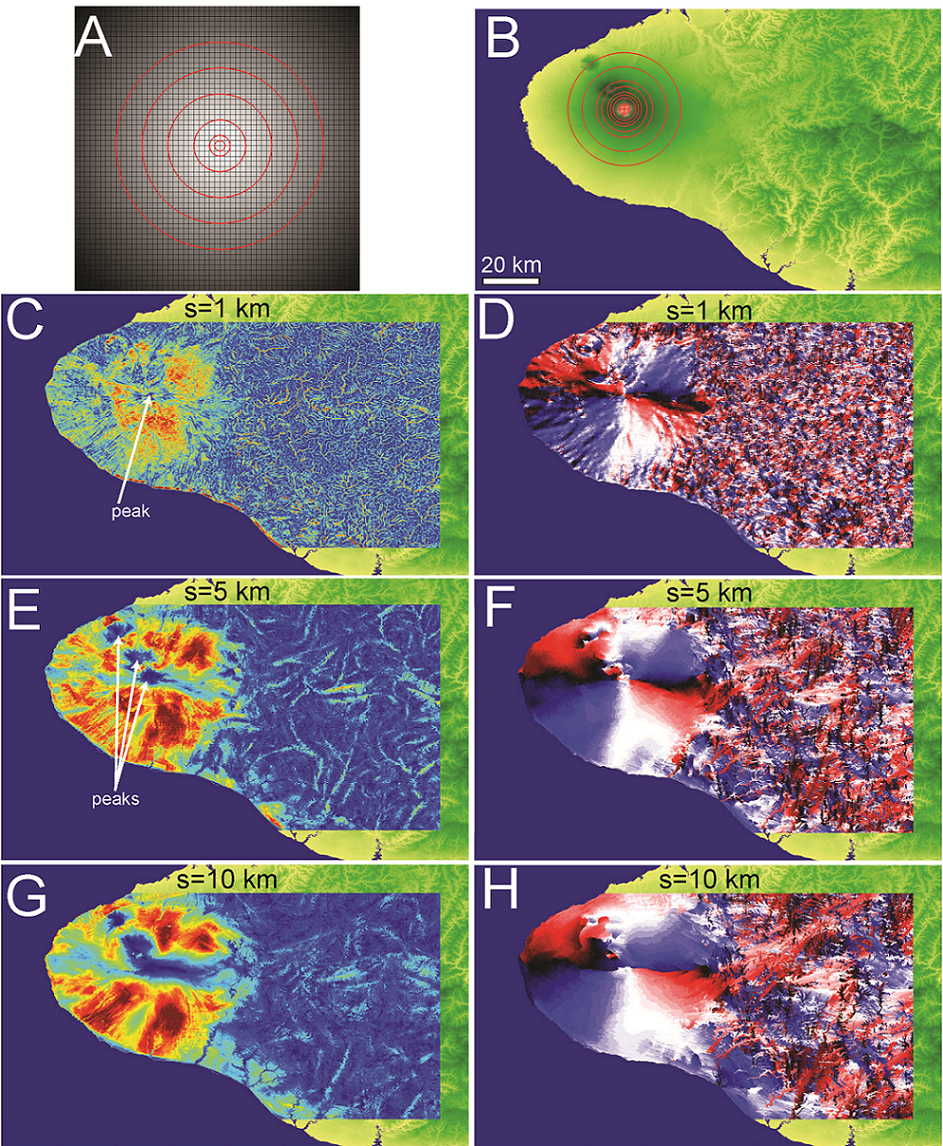
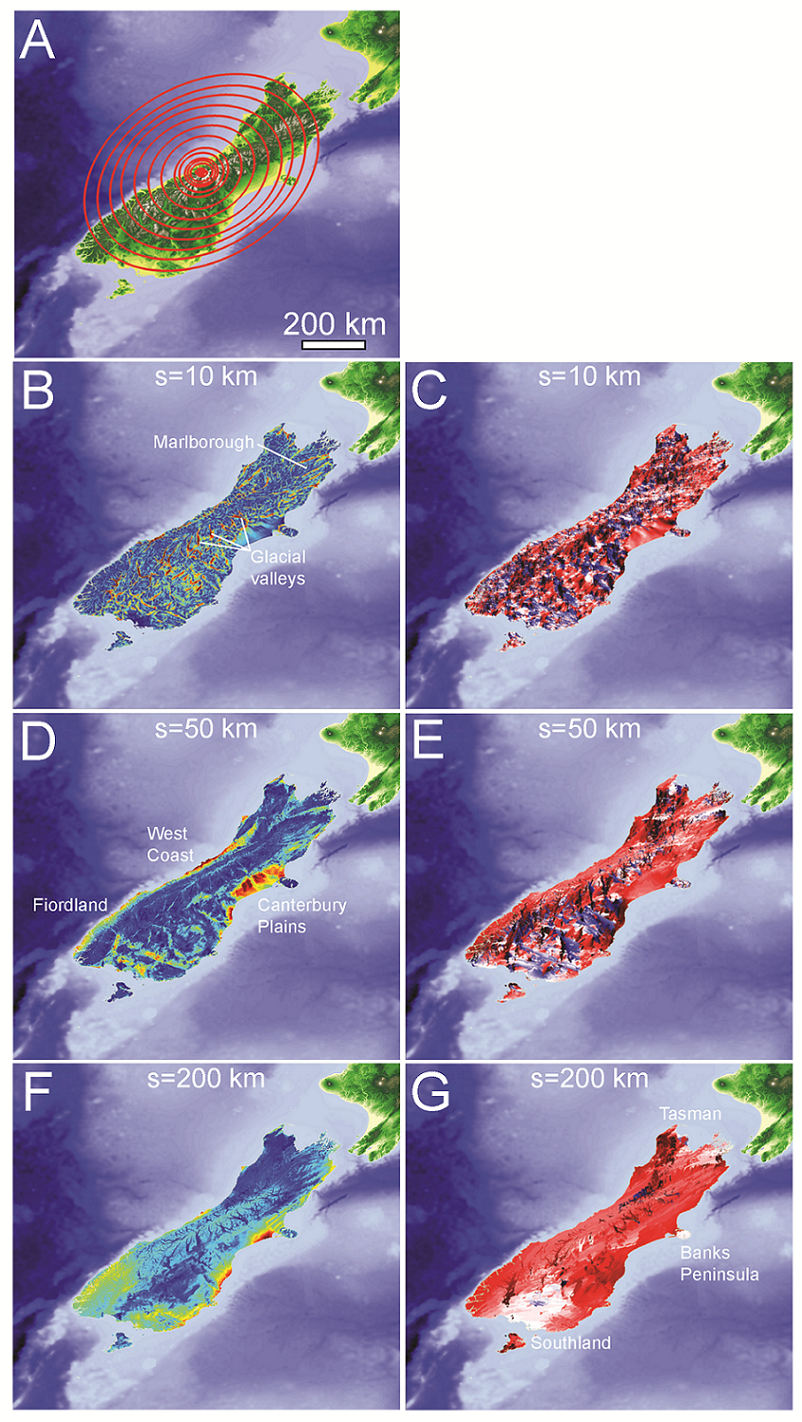
Abstract: We present a method for quantifying orientation and scale dependence of topographic anisotropy to aid in differentiation of the fluvial and tectonic contributions to surface evolution. Using multi-directional variogram statistics to track the spatial persistence of elevation values across a landscape, we calculate anisotropy as a multiscale, direction-sensitive variance in elevation between two points on a surface. Tectonically derived topographic anisotropy is associated with the three-dimensional kinematic field, which contributes 1) differential surface displacement and 2) crustal weakening along shear zones, both of which amplify processes of surface erosion. Based on our analysis, tectonic displacements dominate the topographic field at the scale of mountain ranges, while a combination of the local displacement and strength fields are well represented at the ridge and valley scale. Drainage network patterns tend to reflect the geometry of underlying active or inactive tectonic structures due to the rapid erosion of faults and differential displacement across the fault. The persistence and complexity of correlated anisotropic signals depends on how the strain field evolves with time: new tectonic regimes can overprint the original topographic signal, or the signal can slowly recede as tectonism halts. Regions that have been largely devoid of strain, such as passive coastal margins, have predominantly isotropic topography with typically dendritic drainage network patterns. These methods can be used successfully to infer the settings of past or present tectonic regimes, and can be particularly useful in predicting the location and orientation of structural features that would otherwise be impossible to interpret in the field.




S.G. Roy (a), P.O. Koons (a), B. Osti (a), P. Upton (b), G.E. Tucker (c)

a Earth and Climate Sciences, University of Maine
b GNS Science
c Cooperative Institute for Research in Environmental Sciences (CIRES) and Department of Geological Sciences, University of Colorado

NSF-CDI-1027809

Retrieved from "http://wiki.geodynamics.umaine.edu/index.php?title=Topographic_Anisotropy&oldid=4515"