Difference between revisions of "Transition to Turbulence"
| Line 3: | Line 3: | ||
In this module, you will learn how viscosity affects the dynamics of a simple fluid system with a single cylindrical impediment placed in the flow path. Our tools in this endeavor are [https://www.comsol.com/ COMSOL Multiphysics] and [https://www.paraview.org/ ParaView]. At the end of the module, you should be able to describe the initial conditions of a system, the transition from laminar to turbulent flow, and the effect viscosity has on the inertia, complexity, and predictability of a system. | In this module, you will learn how viscosity affects the dynamics of a simple fluid system with a single cylindrical impediment placed in the flow path. Our tools in this endeavor are [https://www.comsol.com/ COMSOL Multiphysics] and [https://www.paraview.org/ ParaView]. At the end of the module, you should be able to describe the initial conditions of a system, the transition from laminar to turbulent flow, and the effect viscosity has on the inertia, complexity, and predictability of a system. | ||
| − | We will | + | We will move from looking at models with higher viscosity regimes and move to lower viscosity. |
First, let's start by learning how to talk about the various components of flow. | First, let's start by learning how to talk about the various components of flow. | ||
= Basics = | = Basics = | ||
| + | |||
| + | When we talk about flow, we need to first describe the fluid. Some of the fundamental characteristics of fluid are density, viscosity, compressibility, heat capacity, and thermal conductivity. In this exercise we will ignore the thermal properties entirely, define constant density and compressibility, but focus most of our attention on how viscosity affects the kinematics of a fluid system. | ||
| + | |||
| + | Compressibility and density are fairly easy to define. Compressibility is the tendency of a fluid to change its volume due to pressure. Water's compressibility is 45 * 10<sup>-11</sup> Pascal seconds (Pa s). For the purposes of this exercise, since we are not dealing with immense pressure, we assume that compressibility is zero. | ||
| + | |||
| + | Density is the quantity of mass per unit volume. Water's density is 1000 kilograms per cubic meter. Both compressibility and density will be constant throughout our model runs. | ||
| + | |||
| + | These parameters will be fed into the Navier-Stokes fluid momentum equation (below) for each location in the model at each time step. | ||
| + | |||
| + | === Navier-Stokes momentum equation === | ||
| + | ==== ∂v / ∂t = ρg + µ∇<sup>2</sup>U - ∇P ==== | ||
| + | |||
| + | {| class="wikitable" style="" | ||
| + | !colspan=2|where | ||
| + | |- | ||
| + | |'''∂v''' | ||
| + | |= change in velocity | ||
| + | |- | ||
| + | |'''∂t''' | ||
| + | |= change in time | ||
| + | |- | ||
| + | |'''ρ''' | ||
| + | |= density | ||
| + | |- | ||
| + | |'''g''' | ||
| + | |= acceleration due to gravity | ||
| + | |- | ||
| + | |'''µ''' | ||
| + | |= viscosity | ||
| + | |- | ||
| + | |'''∇<sup>2</sup>U''' | ||
| + | |= divergence of velocity (gradient) | ||
| + | |- | ||
| + | |'''∇P''' | ||
| + | |= divergence of pressure (gradient) | ||
| + | |} | ||
| + | |||
| + | Since we are looking at viscosity's effect on flow, let's look at the viscosities of fluids we'll be working with. | ||
| + | |||
| + | {| class="wikitable" style="" | ||
| + | !Fluid | ||
| + | !µ (viscosity) | ||
| + | |- | ||
| + | |'''Honey''' | ||
| + | |1 * 10<sup>1.5</sup> Pa s | ||
| + | |- | ||
| + | |'''Water''' | ||
| + | |1 * 10<sup>-3</sup> Pa s | ||
| + | |- | ||
| + | |'''Air''' | ||
| + | |1 * 10<sup>-5</sup> Pa s | ||
| + | |} | ||
= Model = | = Model = | ||
| + | |||
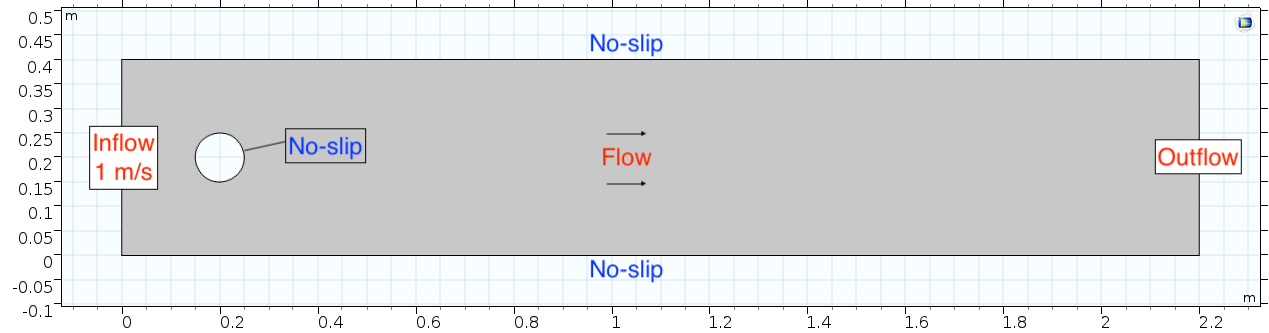
| + | Below is the geometry of our simple COMSOL model. | ||
| + | |||
| + | [[File:Geometry of cylinder model.png]] | ||
| + | |||
| + | This is a two-dimensional COMSOL model, which assumes that the channel is of infinite depth and thus does not produce drag from the bottom of the flow in any way. Both the horizontal (long) walls and the walls of the cylinder have a "no slip" condition. This means that as the flow gets closer to the wall, velocity goes to zero. This condition sets up a velocity gradient between the walls at zero and the center of the flow. The wall on the far left side has an inflow condition of 1 meter per second, and the wall on the right side has a zero-pressure outlet condition, which lets flow pass out of the model unhindered. | ||
| + | |||
| + | When we run the model, we are executing a variation of the Navier-Stokes momentum equation for each mesh element of the model at each time step. This equation, shown below, is fundamental to describing the behavior of fluids in continuum mechanics. | ||
== Honey (μ = 10<sup>1.5</sup> Pa s) == | == Honey (μ = 10<sup>1.5</sup> Pa s) == | ||
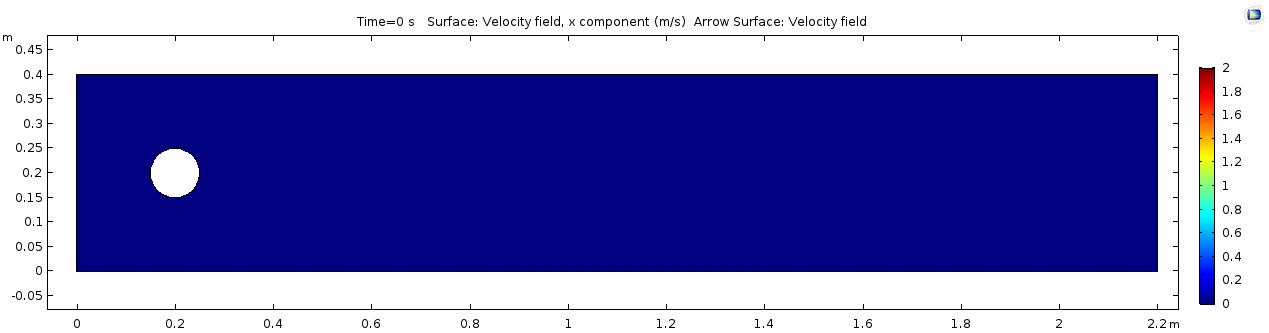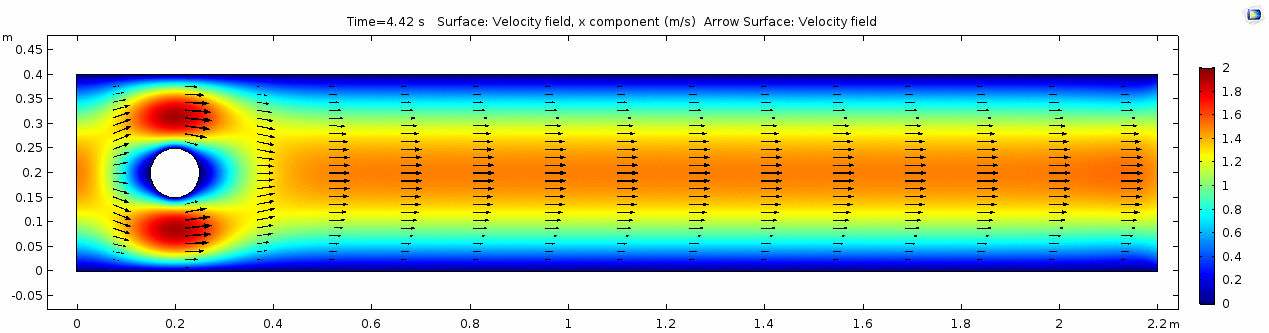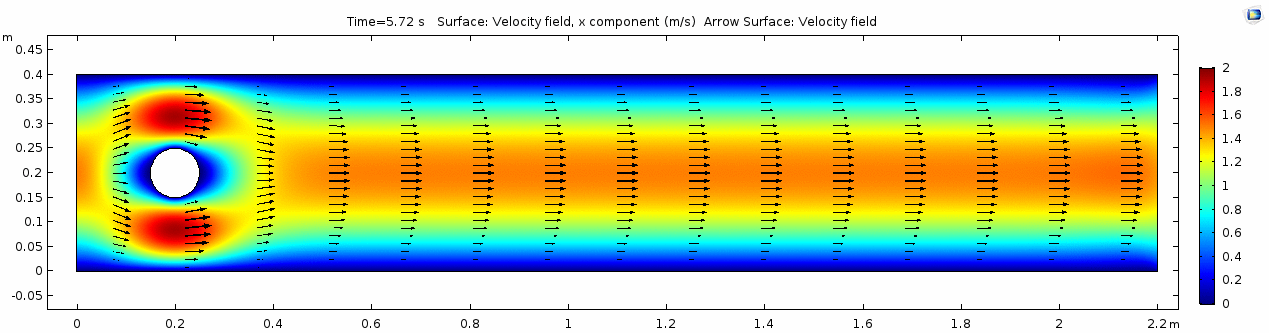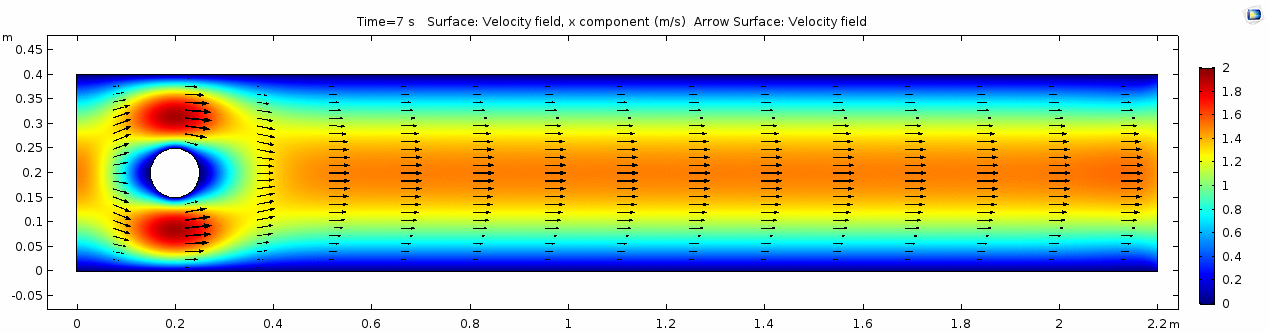
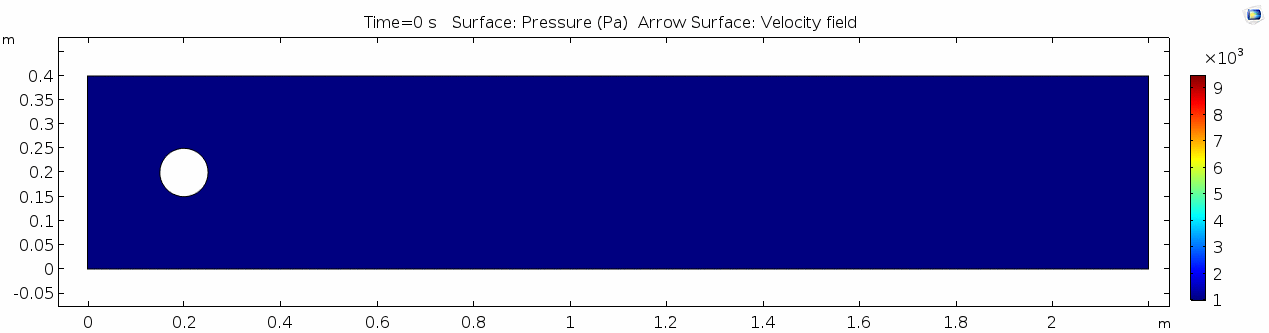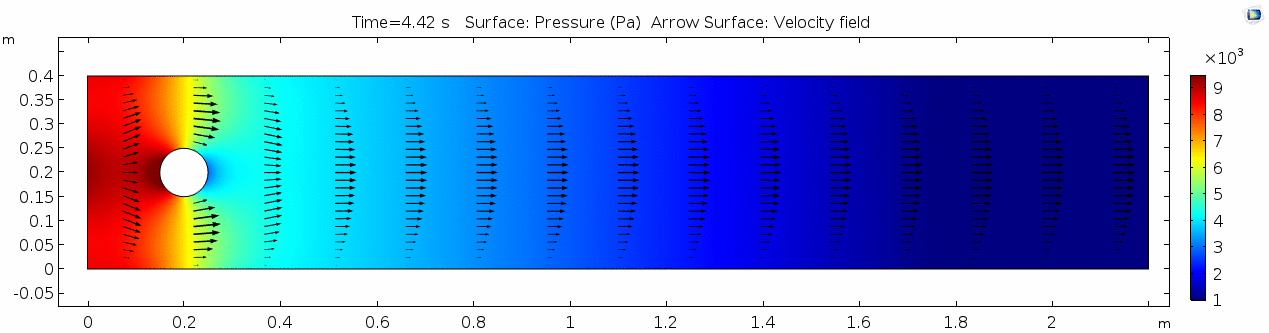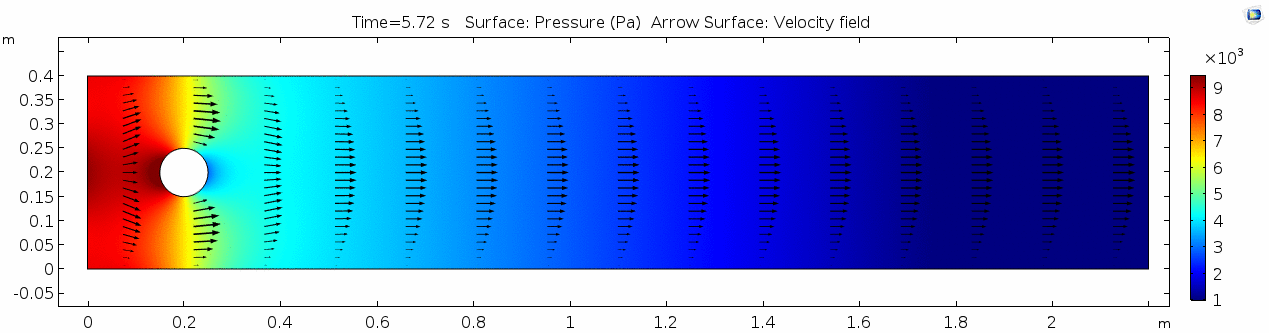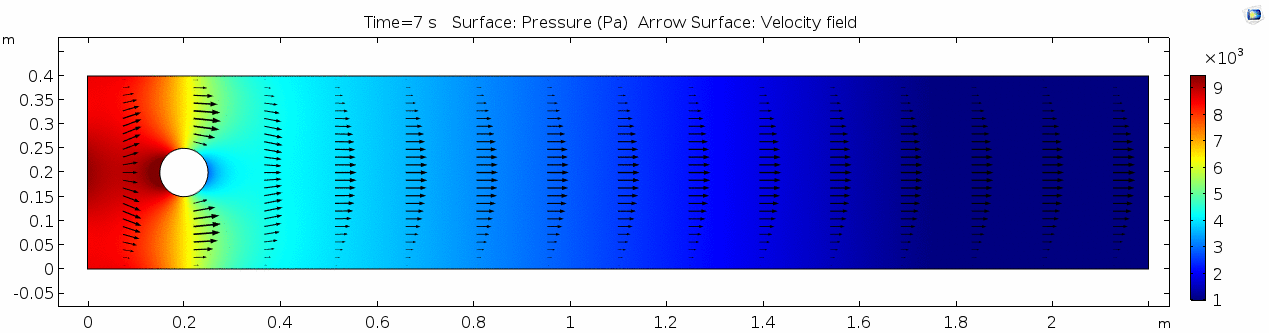
| − | In the first example, we have a fluid with the viscosity of about that of honey, 10<sup>1.5</sup> Pascal seconds (Pa s). | + | In the first example, we have a fluid with the viscosity of about that of honey, 10<sup>1.5</sup> Pascal seconds (Pa s). You might imagine honey to be pretty "sticky," which has something to do with its viscosity. What do you think will happen? Let's look at a few parameters of flow in the honey model. |
=== Velocity field === | === Velocity field === | ||
[[File:Mu101.5_ux1_velocity.gif]] | [[File:Mu101.5_ux1_velocity.gif]] | ||
| + | |||
| + | So, things are pretty orderly and logical here. Not a whole lot changes over time. You might describe this flow system as "'''laminar'''," since you can describe what will happen at any given point in the model space at any given time fairly easily. Note that velocity is highest near the cylinder where the honey must "squeeze by" the cylinder in order to keep up with the 1 m s<sup>-1</sup> inflow rate. This sets up a steep velocity gradient near the no-slip boundary of the cylinder, which we can see in the shear rate: | ||
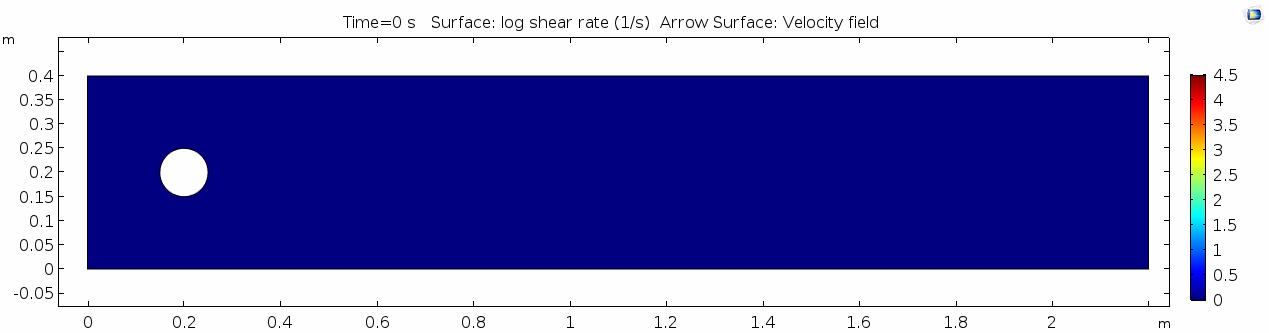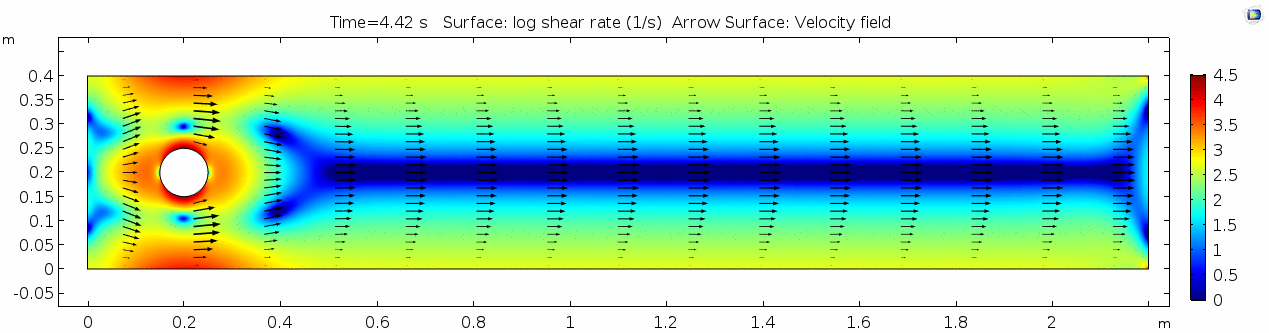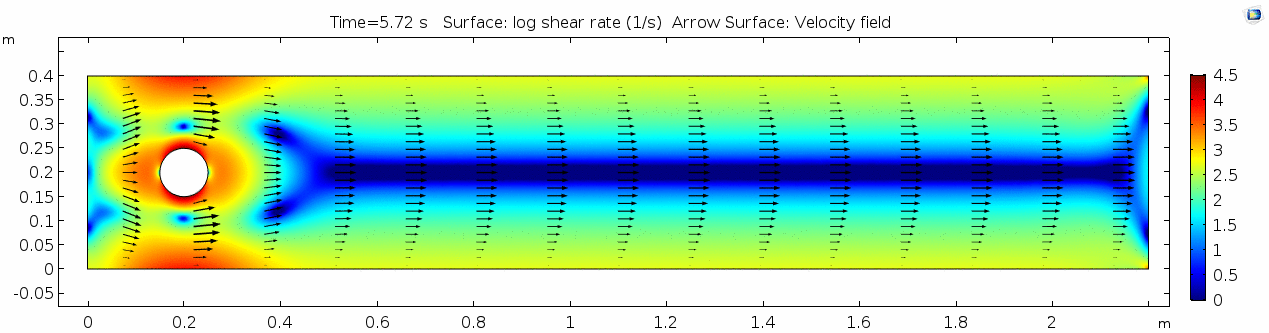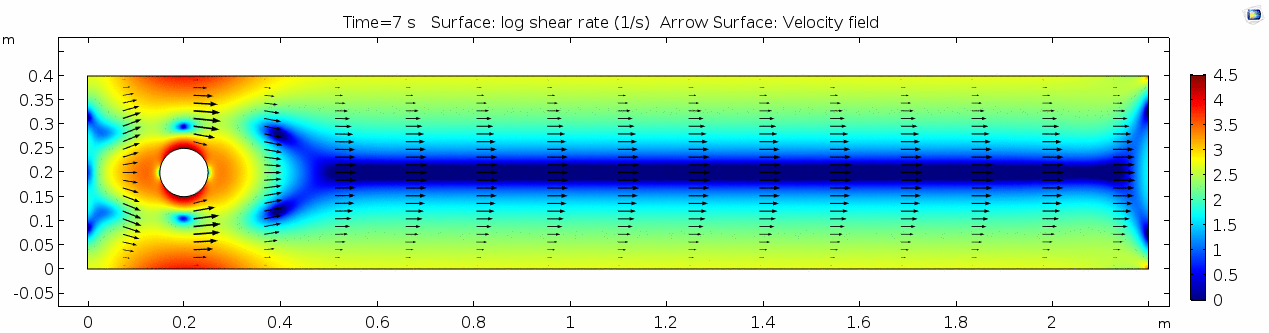
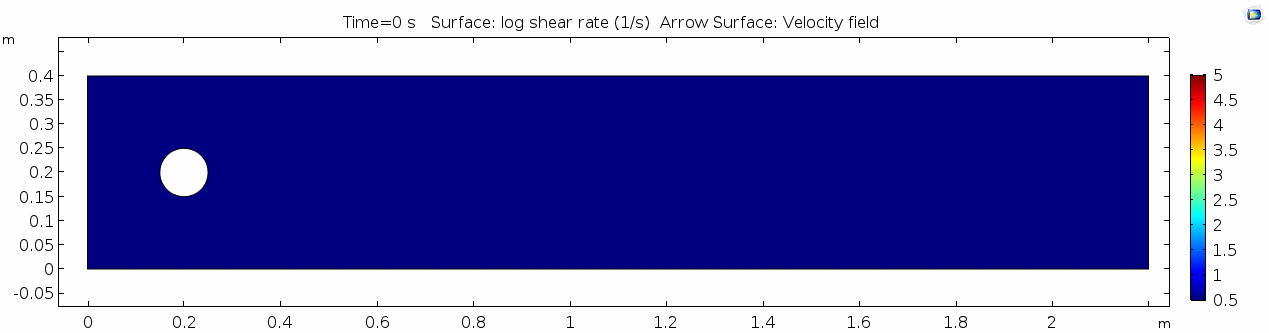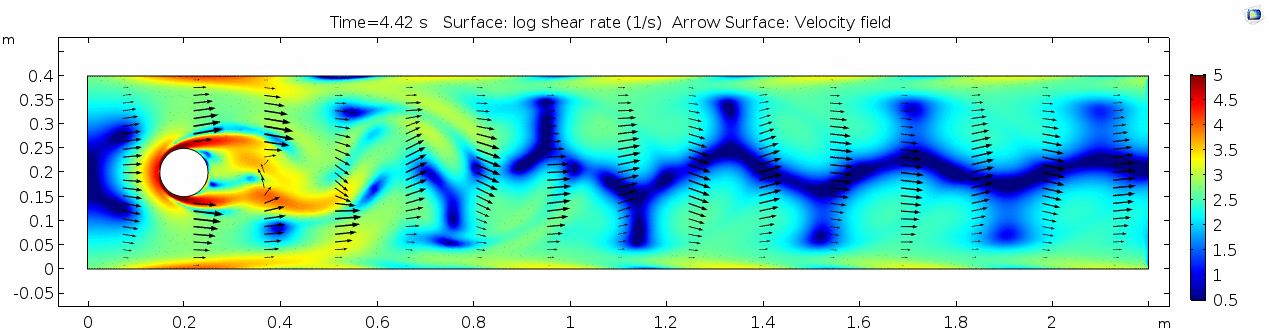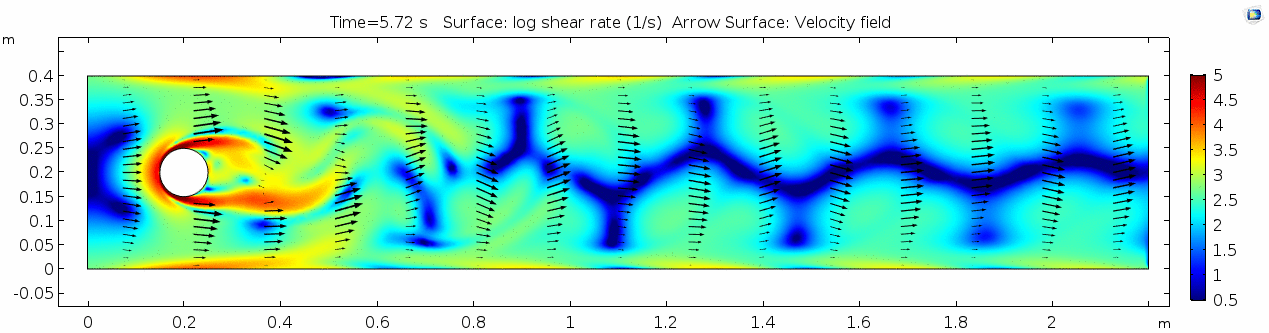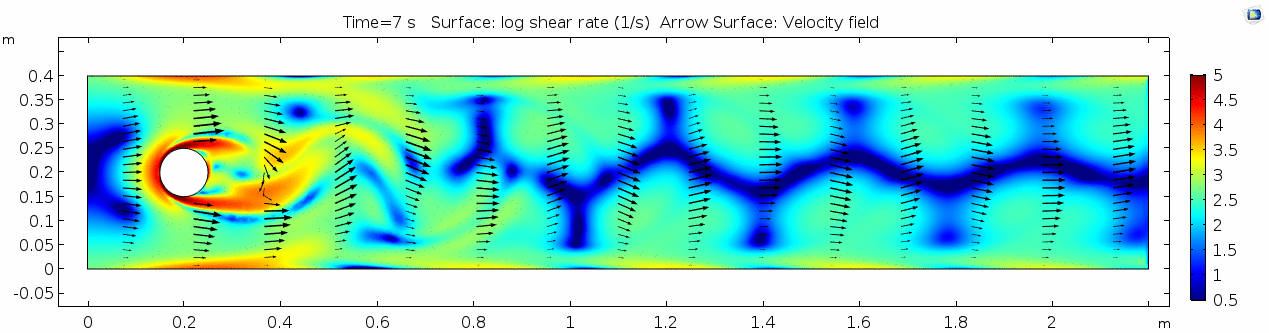
=== Shear rate === | === Shear rate === | ||
[[File:Mu101.5 ux1 shear.gif]] | [[File:Mu101.5 ux1 shear.gif]] | ||
| + | |||
| + | Shear rate is by definition the derivative of the velocity field, so it is no surprise that the highest shear values are in the areas next to the cylinder where the steep velocity gradient exists. If we break shear down into its component parts, we get vorticity, or the curl of the velocity field: | ||
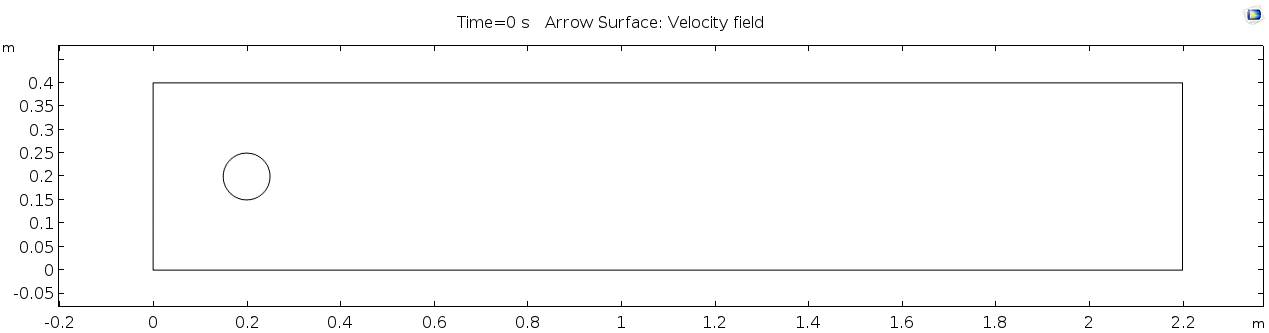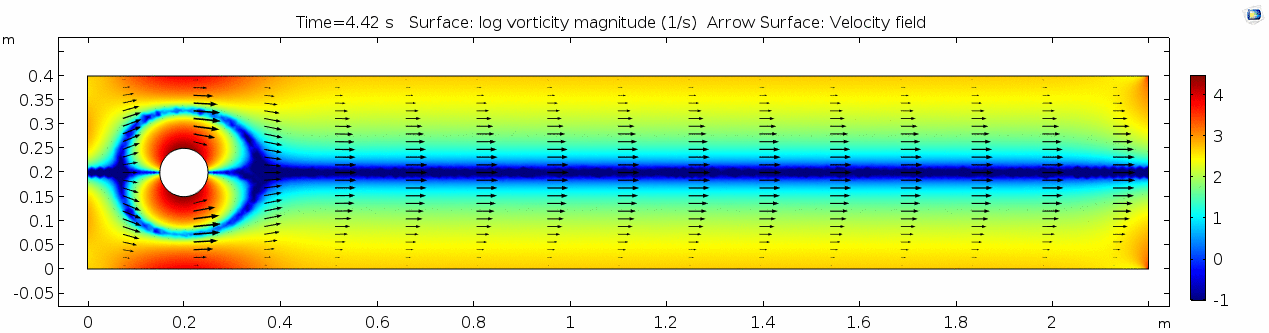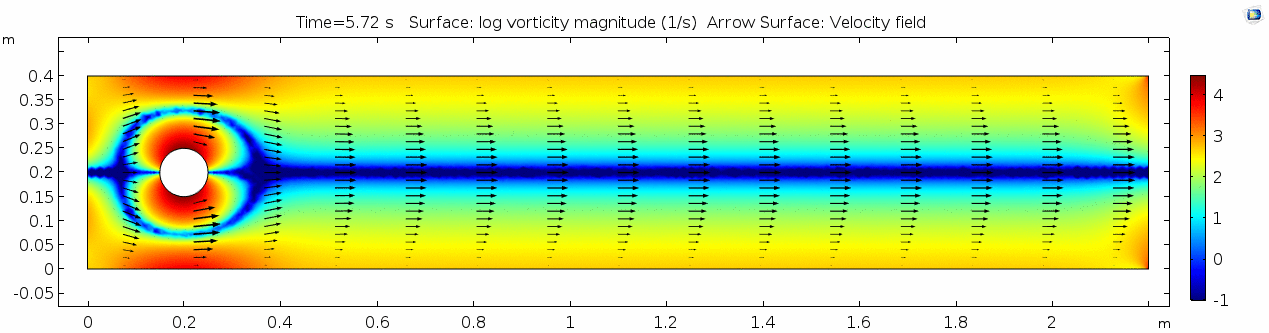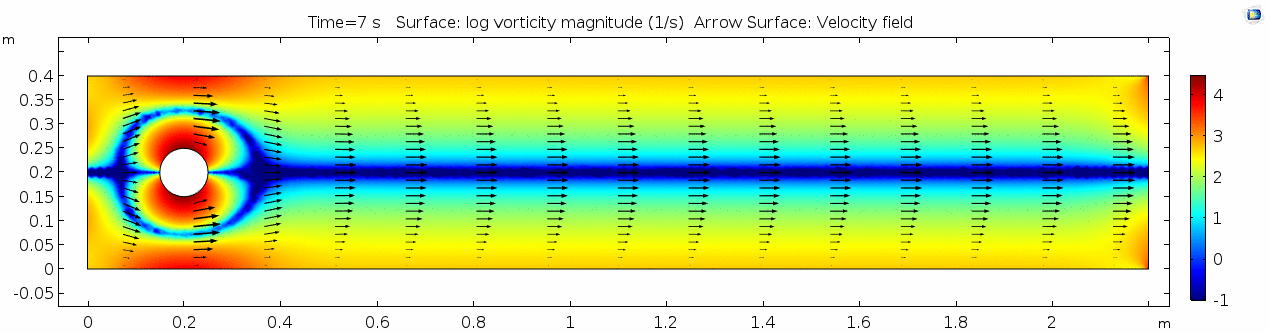
=== Vorticity magnitude === | === Vorticity magnitude === | ||
[[File:Mu101.5 ux1 vorticity.gif]] | [[File:Mu101.5 ux1 vorticity.gif]] | ||
| + | |||
| + | Again, unsurprisingly, the curl is highest where the gradient of velocity is high. This makes sense because as two particles slip past each other at different velocities, their orientation changes (rotates) with regards to one another. Vorticity will be highest near the no-slip boundaries in a simple laminar system like this. | ||
| + | |||
| + | === Pressure === | ||
| + | [[File:Mu101.5 ux1 pressure.gif]] | ||
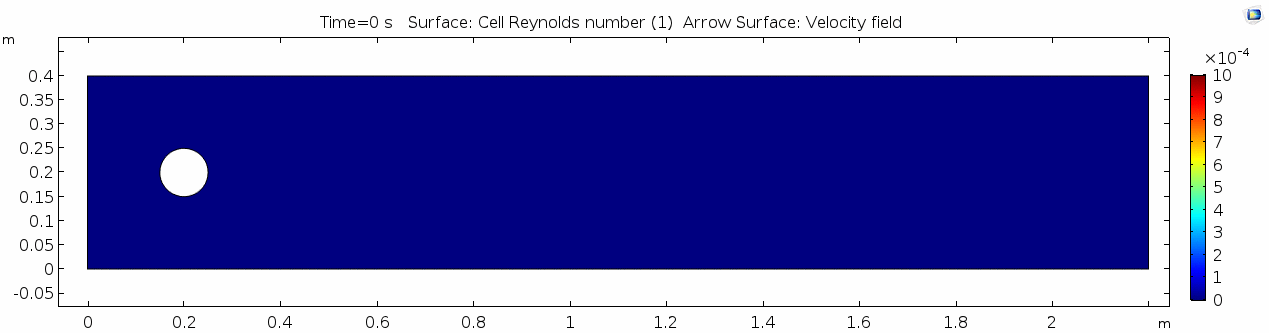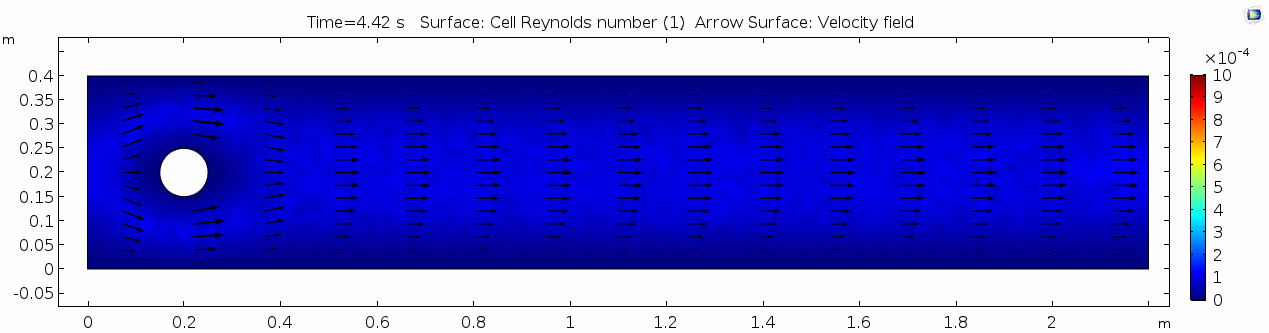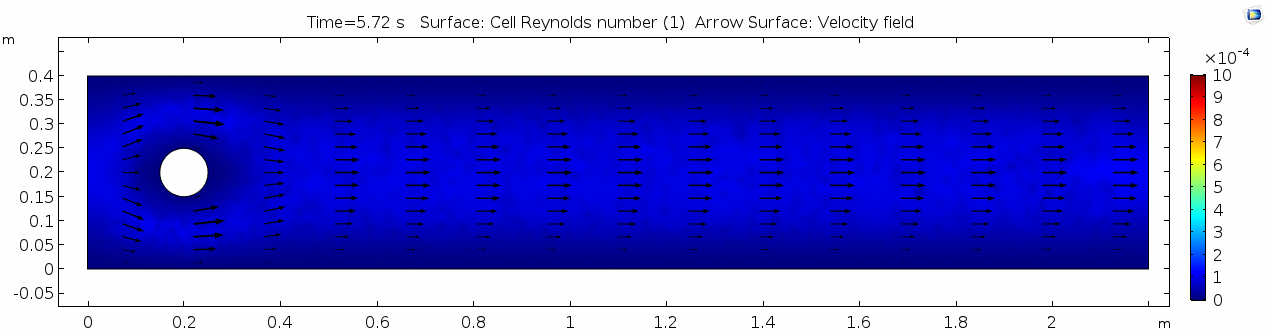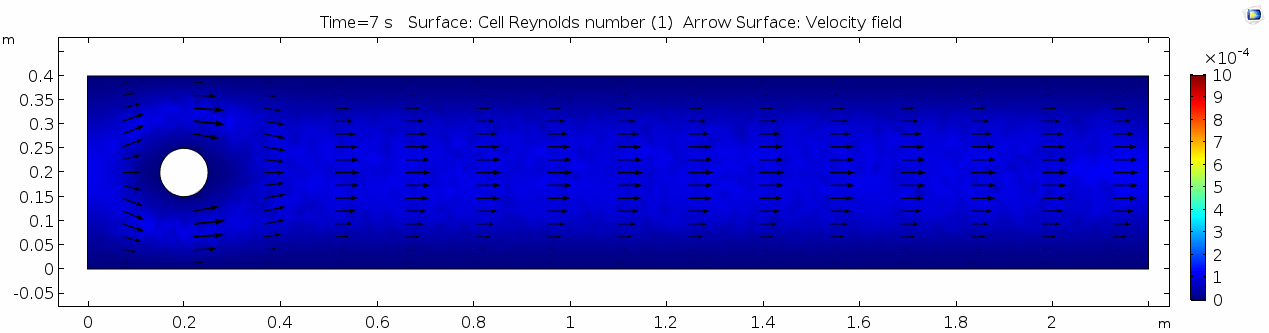
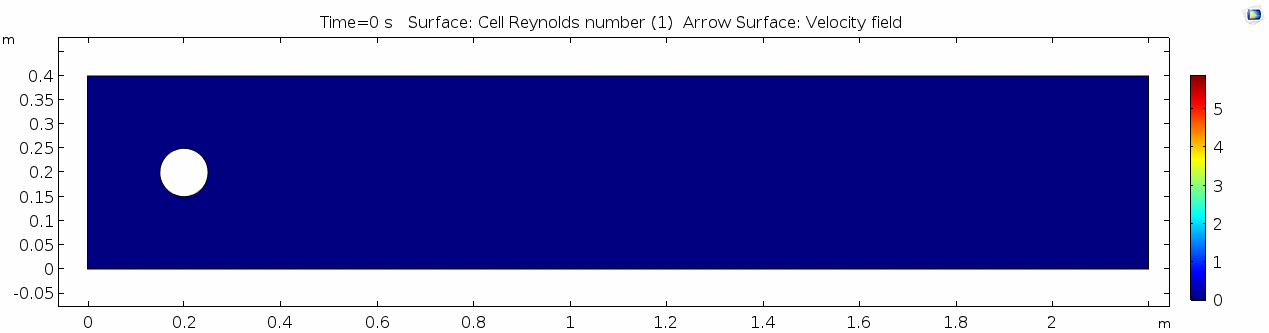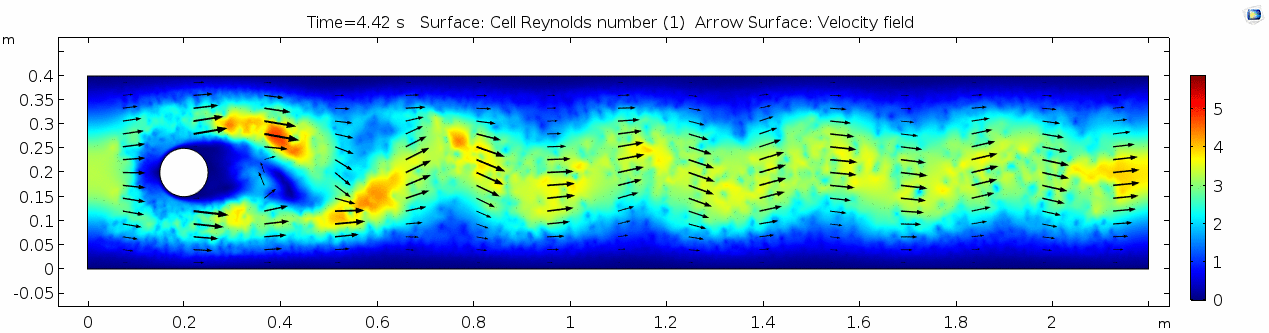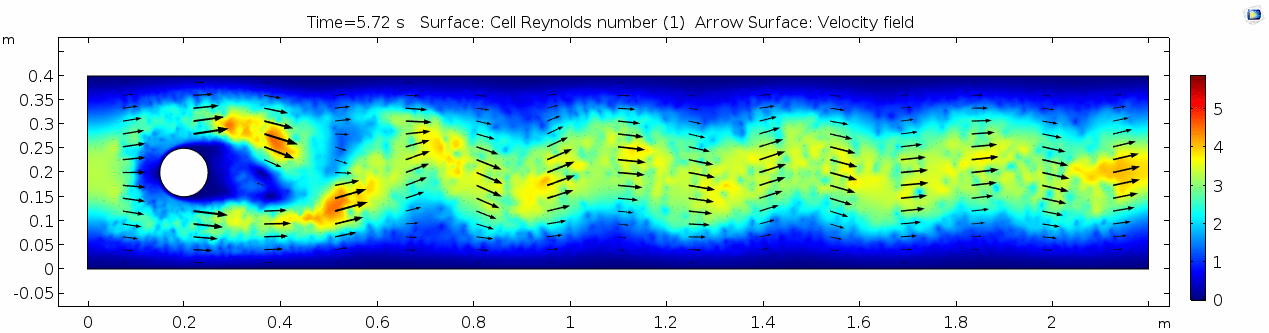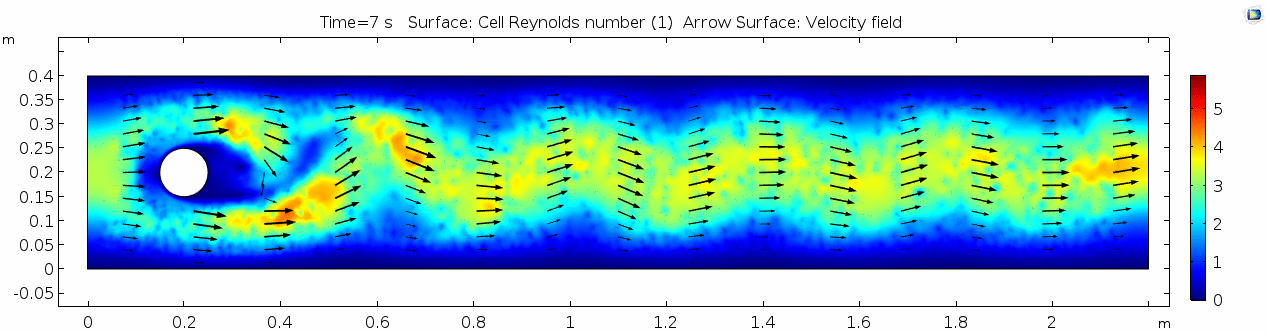
=== Reynolds number === | === Reynolds number === | ||
[[File:Mu101.5 ux1 reynolds.gif]] | [[File:Mu101.5 ux1 reynolds.gif]] | ||
| + | |||
| + | Reynolds number | ||
| + | |||
| + | |||
| + | |||
| + | === Discussion === | ||
| + | |||
| + | Okay, so what's happening here? Things look pretty "boring" so far. With the exception of the very first frame in which the fluid has not begun to move yet, all of the frames are visually nearly the same. As you can tell by the color scale on the velocity plot, the fluid is moving as fast as 1.8 m s<sup>-1</sup> past the cylinder, but apart from that, there seems to be no instability here. This system is the result of '''kinematic''' forces at work, but the system seems to be stable, i.e. there is very little '''dynamic''' element to this system. Another way to say this is that there is not much variance in any given cell through time. | ||
| + | |||
| + | |||
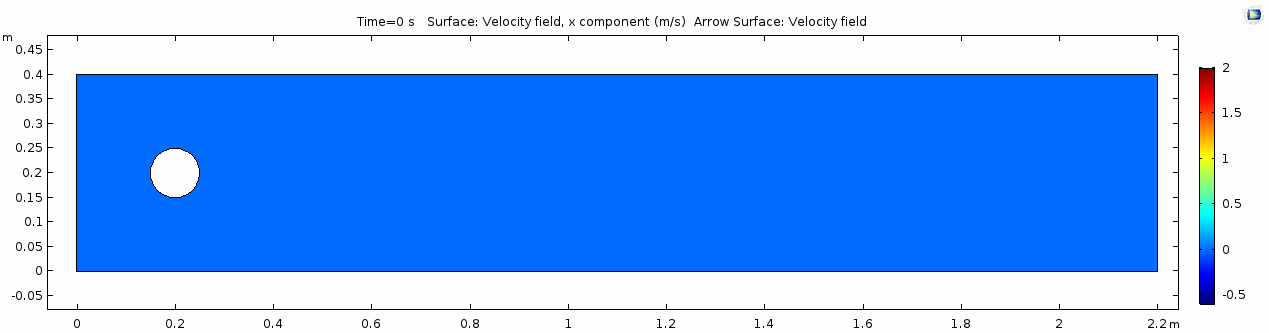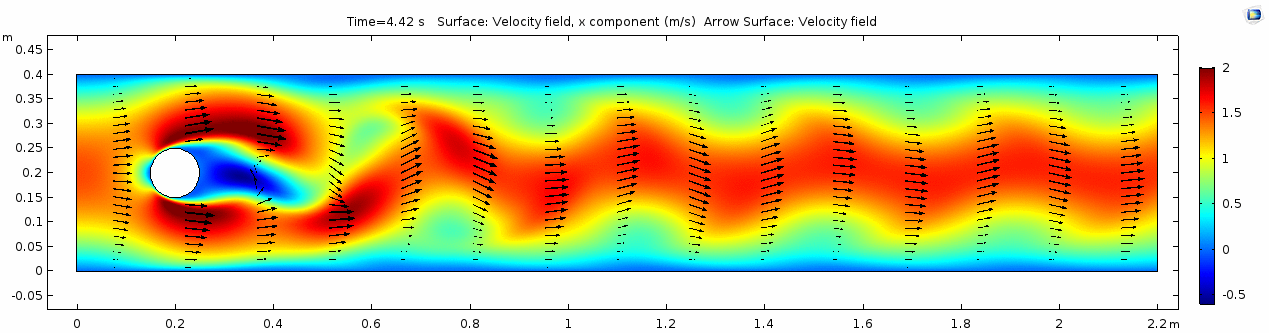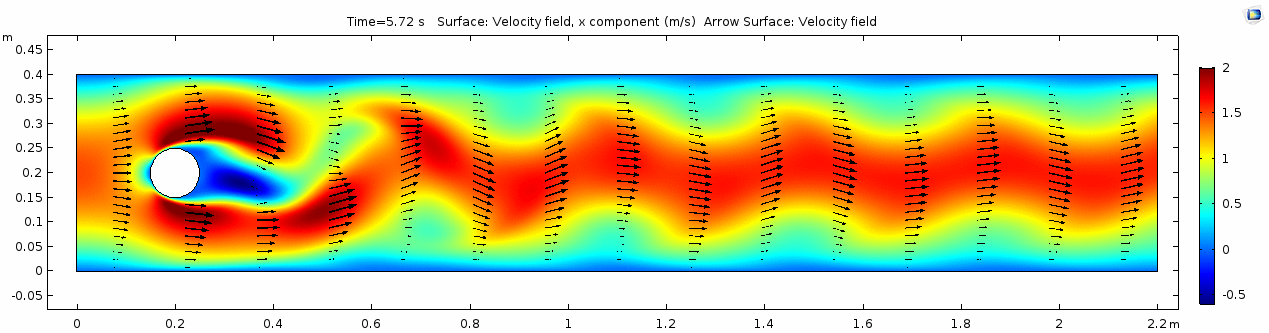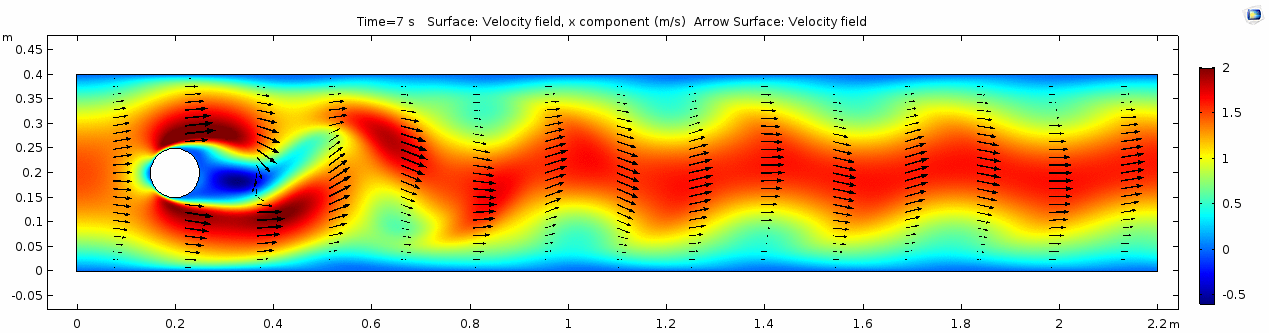
| + | == Water (μ = 10<sup>-3</sup> Pa s) == | ||
| + | |||
| + | === Velocity field === | ||
| + | [[File:Mu10-3_ux1_velocity.gif]] | ||
| + | |||
| + | === Shear rate === | ||
| + | [[File:Mu10-3 ux1 shear.gif]] | ||
| + | |||
| + | === Vorticity magnitude === | ||
| + | [[File:Mu10-3 ux1 vorticity.gif]] | ||
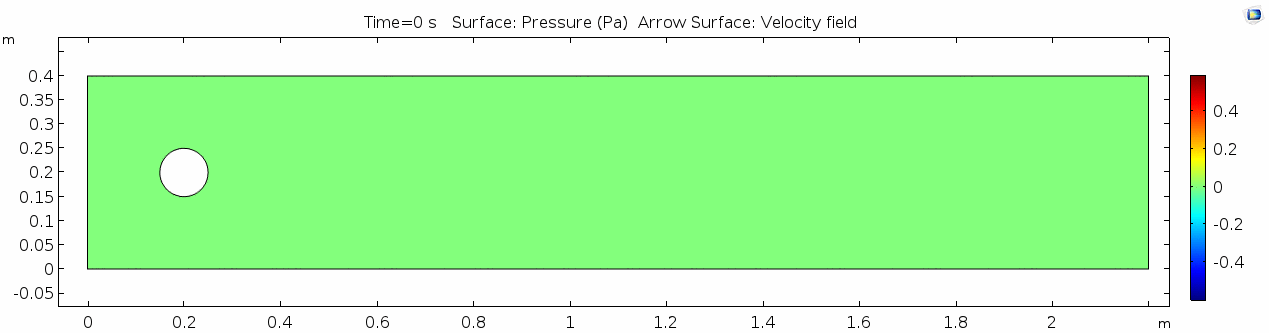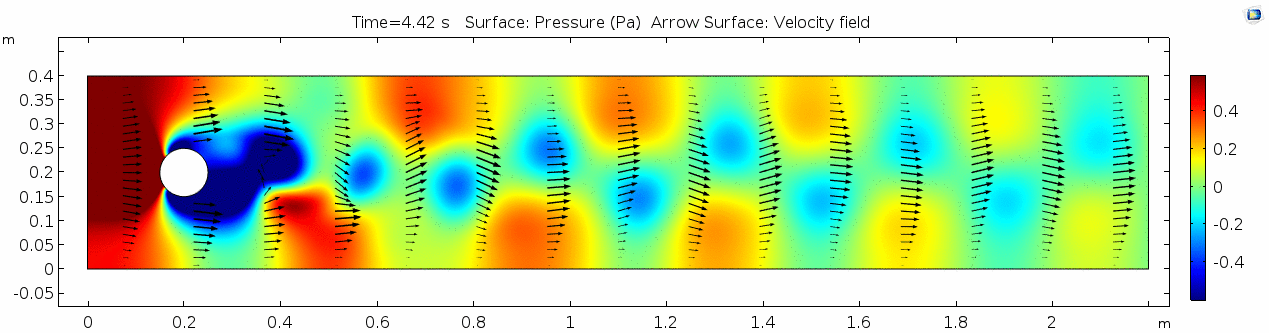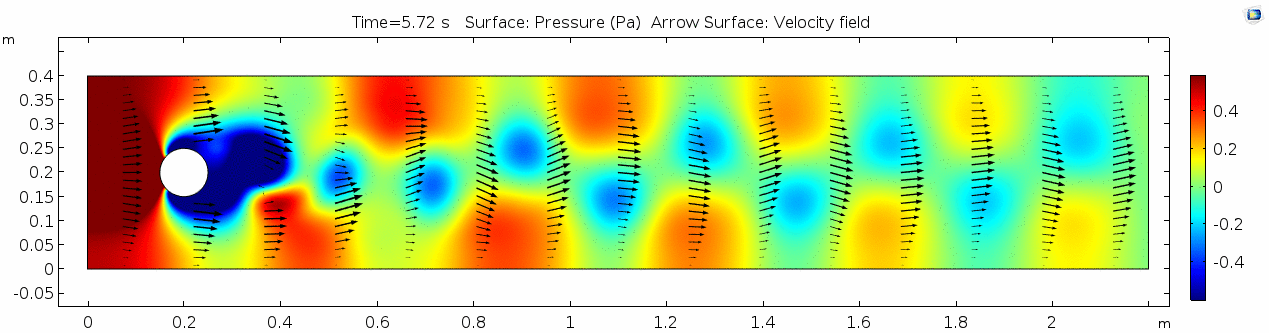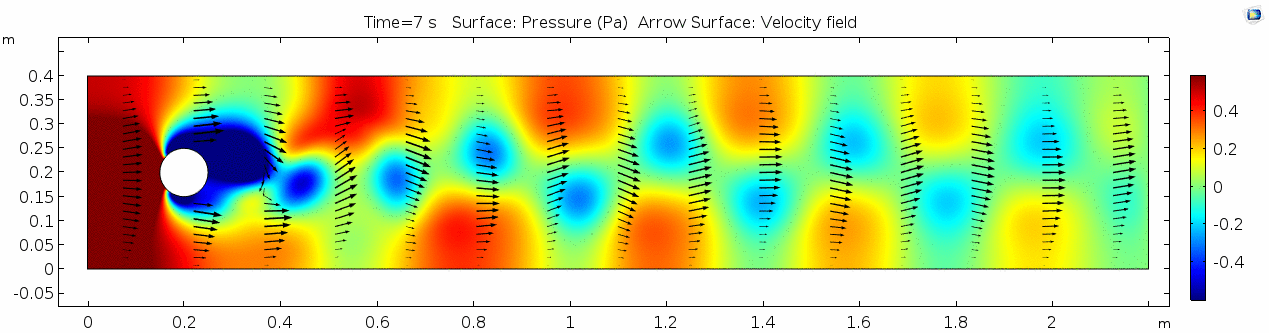
=== Pressure === | === Pressure === | ||
| − | [[File: | + | [[File:Mu10-3 ux1 pressure.gif]] |
| + | === Reynolds number === | ||
| + | [[File:Mu10-3 ux1 reynolds.gif]] | ||
| − | |||
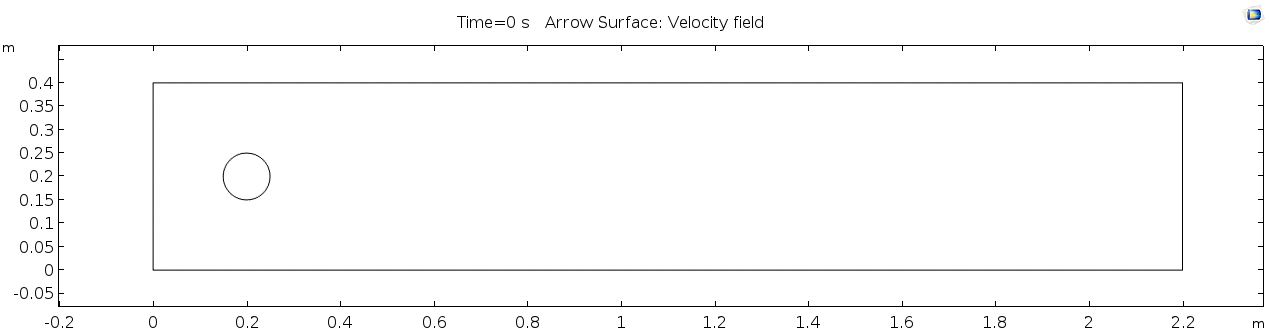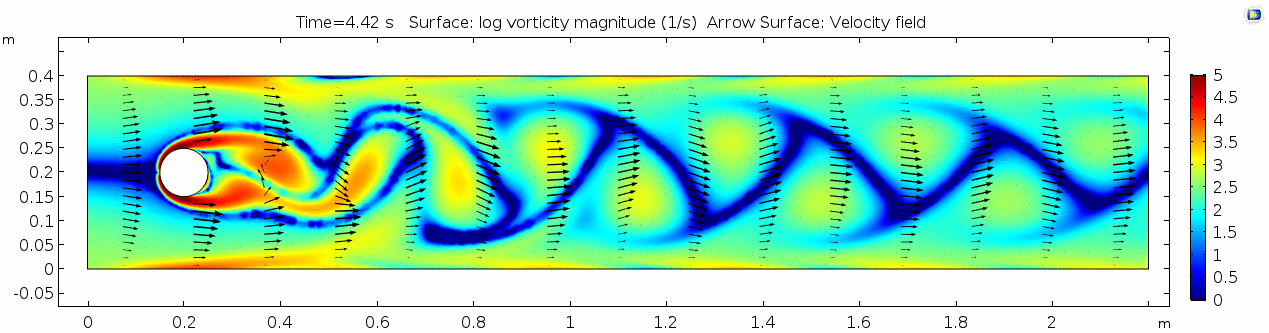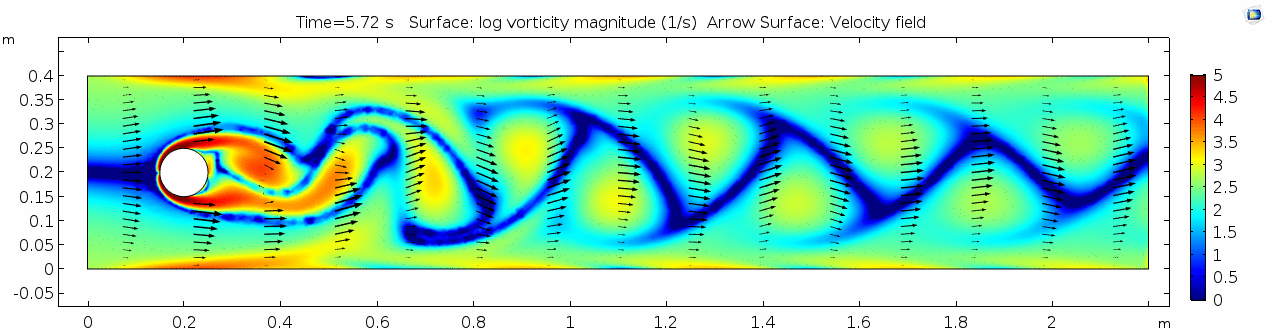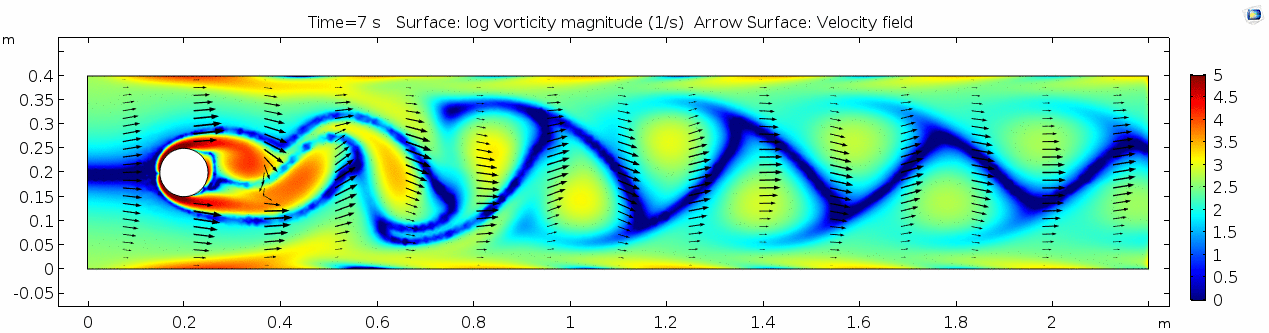
== Air (μ = 10<sup>-5</sup> Pa s) == | == Air (μ = 10<sup>-5</sup> Pa s) == | ||
Revision as of 20:48, 21 February 2019
Created by Ian Nesbitt and Jukes Liu on 2019-02-19
In this module, you will learn how viscosity affects the dynamics of a simple fluid system with a single cylindrical impediment placed in the flow path. Our tools in this endeavor are COMSOL Multiphysics and ParaView. At the end of the module, you should be able to describe the initial conditions of a system, the transition from laminar to turbulent flow, and the effect viscosity has on the inertia, complexity, and predictability of a system.
We will move from looking at models with higher viscosity regimes and move to lower viscosity.
First, let's start by learning how to talk about the various components of flow.
Basics
When we talk about flow, we need to first describe the fluid. Some of the fundamental characteristics of fluid are density, viscosity, compressibility, heat capacity, and thermal conductivity. In this exercise we will ignore the thermal properties entirely, define constant density and compressibility, but focus most of our attention on how viscosity affects the kinematics of a fluid system.
Compressibility and density are fairly easy to define. Compressibility is the tendency of a fluid to change its volume due to pressure. Water's compressibility is 45 * 10-11 Pascal seconds (Pa s). For the purposes of this exercise, since we are not dealing with immense pressure, we assume that compressibility is zero.
Density is the quantity of mass per unit volume. Water's density is 1000 kilograms per cubic meter. Both compressibility and density will be constant throughout our model runs.
These parameters will be fed into the Navier-Stokes fluid momentum equation (below) for each location in the model at each time step.
∂v / ∂t = ρg + µ∇2U - ∇P
| where | |
|---|---|
| ∂v | = change in velocity |
| ∂t | = change in time |
| ρ | = density |
| g | = acceleration due to gravity |
| µ | = viscosity |
| ∇2U | = divergence of velocity (gradient) |
| ∇P | = divergence of pressure (gradient) |
Since we are looking at viscosity's effect on flow, let's look at the viscosities of fluids we'll be working with.
| Fluid | µ (viscosity) |
|---|---|
| Honey | 1 * 101.5 Pa s |
| Water | 1 * 10-3 Pa s |
| Air | 1 * 10-5 Pa s |
Model
Below is the geometry of our simple COMSOL model.
This is a two-dimensional COMSOL model, which assumes that the channel is of infinite depth and thus does not produce drag from the bottom of the flow in any way. Both the horizontal (long) walls and the walls of the cylinder have a "no slip" condition. This means that as the flow gets closer to the wall, velocity goes to zero. This condition sets up a velocity gradient between the walls at zero and the center of the flow. The wall on the far left side has an inflow condition of 1 meter per second, and the wall on the right side has a zero-pressure outlet condition, which lets flow pass out of the model unhindered.
When we run the model, we are executing a variation of the Navier-Stokes momentum equation for each mesh element of the model at each time step. This equation, shown below, is fundamental to describing the behavior of fluids in continuum mechanics.
Honey (μ = 101.5 Pa s)
In the first example, we have a fluid with the viscosity of about that of honey, 101.5 Pascal seconds (Pa s). You might imagine honey to be pretty "sticky," which has something to do with its viscosity. What do you think will happen? Let's look at a few parameters of flow in the honey model.
Velocity field
So, things are pretty orderly and logical here. Not a whole lot changes over time. You might describe this flow system as "laminar," since you can describe what will happen at any given point in the model space at any given time fairly easily. Note that velocity is highest near the cylinder where the honey must "squeeze by" the cylinder in order to keep up with the 1 m s-1 inflow rate. This sets up a steep velocity gradient near the no-slip boundary of the cylinder, which we can see in the shear rate:
Shear rate
Shear rate is by definition the derivative of the velocity field, so it is no surprise that the highest shear values are in the areas next to the cylinder where the steep velocity gradient exists. If we break shear down into its component parts, we get vorticity, or the curl of the velocity field:
Vorticity magnitude
Again, unsurprisingly, the curl is highest where the gradient of velocity is high. This makes sense because as two particles slip past each other at different velocities, their orientation changes (rotates) with regards to one another. Vorticity will be highest near the no-slip boundaries in a simple laminar system like this.
Pressure
Reynolds number
Reynolds number
Discussion
Okay, so what's happening here? Things look pretty "boring" so far. With the exception of the very first frame in which the fluid has not begun to move yet, all of the frames are visually nearly the same. As you can tell by the color scale on the velocity plot, the fluid is moving as fast as 1.8 m s-1 past the cylinder, but apart from that, there seems to be no instability here. This system is the result of kinematic forces at work, but the system seems to be stable, i.e. there is very little dynamic element to this system. Another way to say this is that there is not much variance in any given cell through time.
Water (μ = 10-3 Pa s)
Velocity field
Shear rate
Vorticity magnitude
Pressure
Reynolds number