Difference between revisions of "Heat transfer module - Fluid Dynamics 2019"
| Line 38: | Line 38: | ||
Where at some critical Rayleigh (Racr) number (dependent on the system), the convection regime shifts | Where at some critical Rayleigh (Racr) number (dependent on the system), the convection regime shifts | ||
| − | Summary: video of the lava lamp annotated with the different steps | + | ''Summary: video of the lava lamp annotated with the different steps |
| + | '' | ||
'''Equations to Know''' | '''Equations to Know''' | ||
| + | |||
''Heat Transfer Equation'': | ''Heat Transfer Equation'': | ||
| + | |||
Describes how heat changes through time | Describes how heat changes through time | ||
[[File:Heat-transfer-2.png]] | [[File:Heat-transfer-2.png]] | ||
| Line 47: | Line 50: | ||
''Peclét Number'': | ''Peclét Number'': | ||
| + | |||
Dimensionless number which indicates whether conduction or advection dominates the system. | Dimensionless number which indicates whether conduction or advection dominates the system. | ||
where u = flow velocity, L = characteristic length Height of lava lamp, κ = thermal diffusivity | where u = flow velocity, L = characteristic length Height of lava lamp, κ = thermal diffusivity | ||
| Line 53: | Line 57: | ||
''Rayleigh Number'': | ''Rayleigh Number'': | ||
| + | |||
Dimensionless number used to describe whether convection grows or decays | Dimensionless number used to describe whether convection grows or decays | ||
Revision as of 00:55, 8 March 2019
HEAT TRANSFER IN A LAVA LAMP
Description When you flip on the light in a lava lamp, heat from the bulb works slowly to warm up the wax (or ‘lava’). This kind of heat transfer is called conduction, or movement of heat from one place to another. Heat energy flows from high heat (light bulb) to low heat (wax), and the gradient is the driver of conductive heat transfer.
Until things start moving, conduction is the dominant heat transfer process in our lava lamp system.
- Conduction depends on:
- thermal diffusivity of the material through which heat is moving
- thermal gradient
The density of the wax is inversely related to temperature, meaning that at higher temperatures, the wax is less dense. When the density becomes lower than the density of the liquid in the lava lamp, the wax will tend to float upward.
Wax reaches critical density (less than liquid) and tends to float upward. That movement of wax introduces velocity into the system--advection.
- Advection depends on:
- velocity of the fluid
- thermal Gradient
Peclet Dimensionless number which indicates whether conduction or advection dominates the system. Drivers of advection are in the numerator and thermal diffusivity, which dominates conduction, is in the denominator. In THIS SYSTEM wax density changes cause velocity, a term in the numerator for the Peclet Introduce heat transfer equation Sketch of advection (first blob moving up), show isotherms and velocity vector With the movement of wax in the upward direction away from the heat source at the bottom of the container and into a cooler material the wax density increases again (more than liquid). This wax density increase causes the wax to sink back down to the bottom of the container towards the heat source. This process is called convection. Convection depends on:
- Driving forces:
- Acceleration due to gravity (g)
- Density (ρ)
- The temperature difference between the bottom and top of the convection cell (ΔT)
- The volume coefficient of thermal expansion (α)
- The height of the convection cell (d)
- Resisting forces:
- Viscosity (μ)
- Thermal diffusivity (κ)
Rayleigh Number Equation Dimensionless number used to describe whether convection grows or decays--dependent upon the driving and resisting forces
- When numerator terms are dominant convection grows
- When denominator terms are dominant convection decays
Where at some critical Rayleigh (Racr) number (dependent on the system), the convection regime shifts
Summary: video of the lava lamp annotated with the different steps
Equations to Know
Heat Transfer Equation:
Describes how heat changes through time
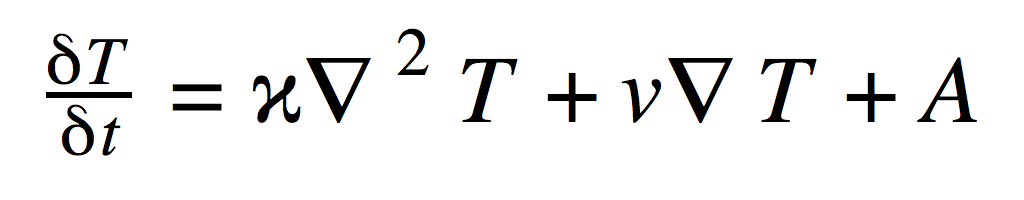
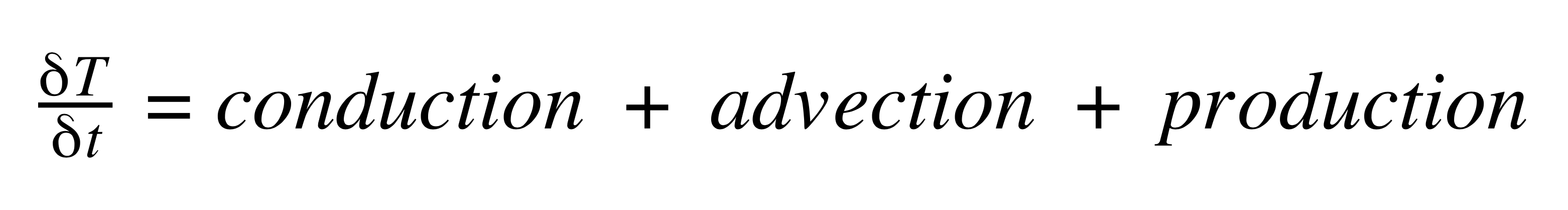
Peclét Number:
Dimensionless number which indicates whether conduction or advection dominates the system.
where u = flow velocity, L = characteristic length Height of lava lamp, κ = thermal diffusivity
- Low peclet regime- dominated by heat transport by conduction
- High peclet regime- dominated by heat transport by advection
Rayleigh Number:
Dimensionless number used to describe whether convection grows or decays
g = acceleration due to gravity ρ = density κ = thermal diffusivity ΔT = the temperature difference between the bottom and top of the convection cell α = the volume coefficient of thermal expansion d = the height of the convection cell μ = viscosity κ = thermal diffusivity
At some critical Rayleigh (Racr) number (dependent on the system), the convection regime shifts
HEAT TRANSFER IN ICE STREAM SHUTDOWN AND START (based on Joughin and Alley, 2011)
Stop and start of ice streams is dependent on: Thinning (steepens basal temperature gradients) Basal freezing (puts on the brakes for a system) Thickening (build up traps geothermal heat) GO & repeat cycle
See video below to walk through the steps of ice stream shut-down and speed-up.
==