Difference between revisions of "Transition to Turbulence"
| Line 1: | Line 1: | ||
| − | ''Created by [[User:Ian|Ian Nesbitt]] on 2019-02-19'' | + | ''Created by [[User:Ian|Ian Nesbitt]] and [[User:Jukes|Jukes Liu]] on 2019-02-19'' |
| + | |||
| + | In this module, you will learn how viscosity affects the dynamics of a simple fluid system with a single cylindrical impediment placed in the flow path. Our tools in this endeavor are [https://www.comsol.com/ COMSOL Multiphysics] and [https://www.paraview.org/ ParaView]. At the end of the module, you should be able to describe the initial conditions of a system, the transition from laminar to turbulent flow, and the effect viscosity has on the inertia, complexity, and predictability of a system. | ||
| + | |||
| + | We will start with a higher viscosity regime and move to lower viscosity. | ||
| + | |||
| + | First, let's start by learning how to talk about the various components of flow. | ||
| + | |||
| + | = Basics = | ||
| + | |||
| + | |||
| + | = Model = | ||
== Honey (μ = 10<sup>1.5</sup> Pa s) == | == Honey (μ = 10<sup>1.5</sup> Pa s) == | ||
| + | |||
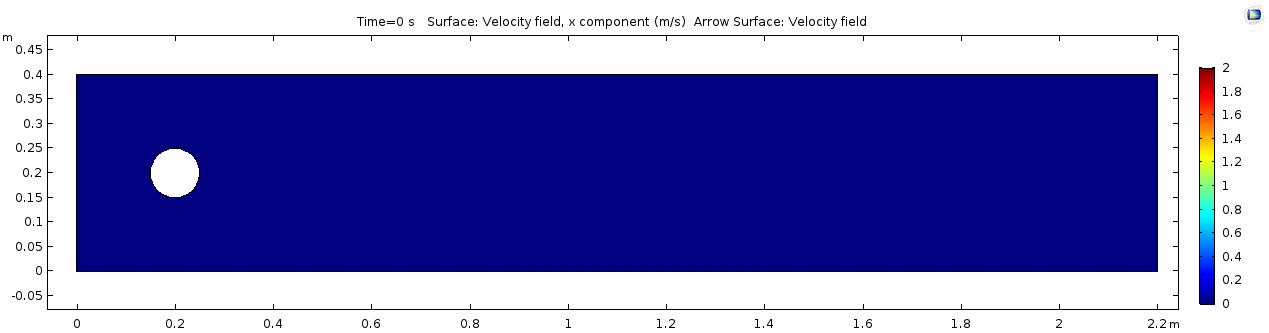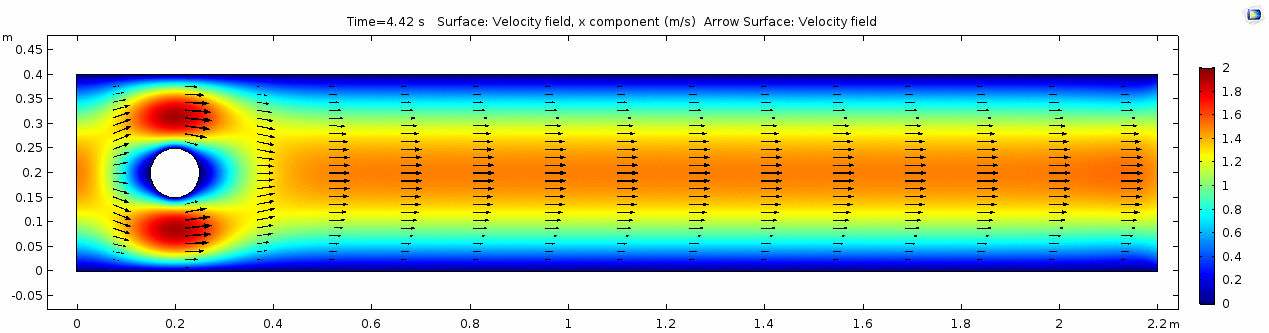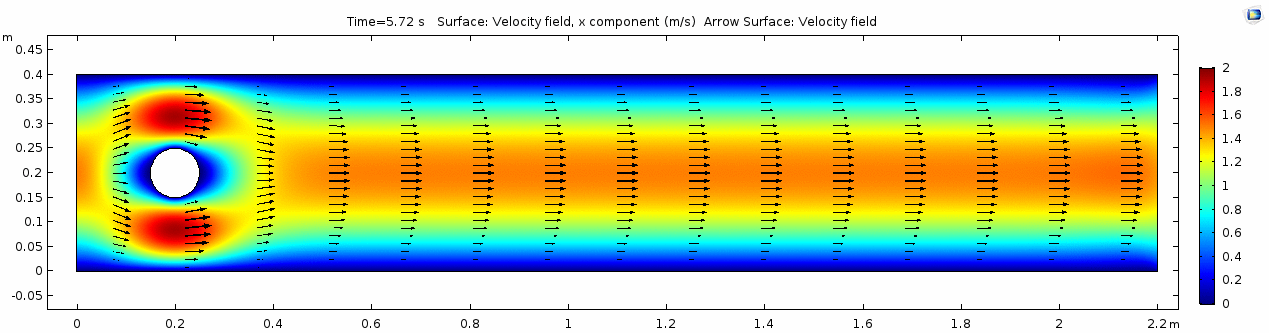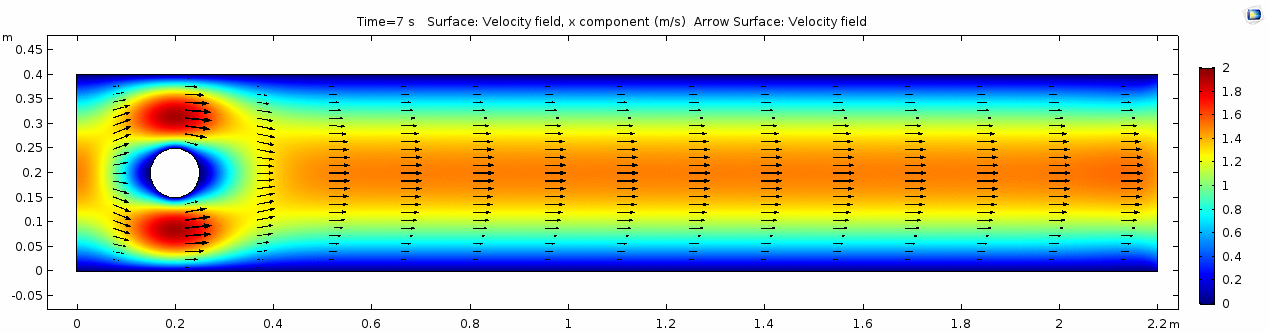
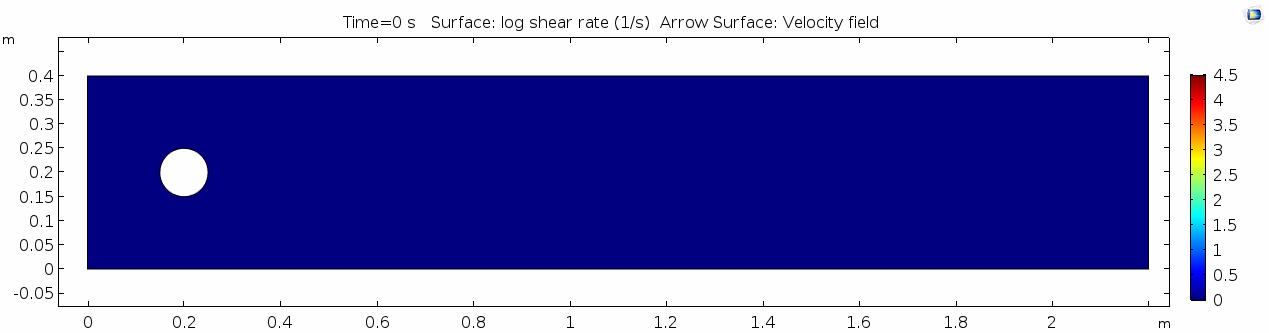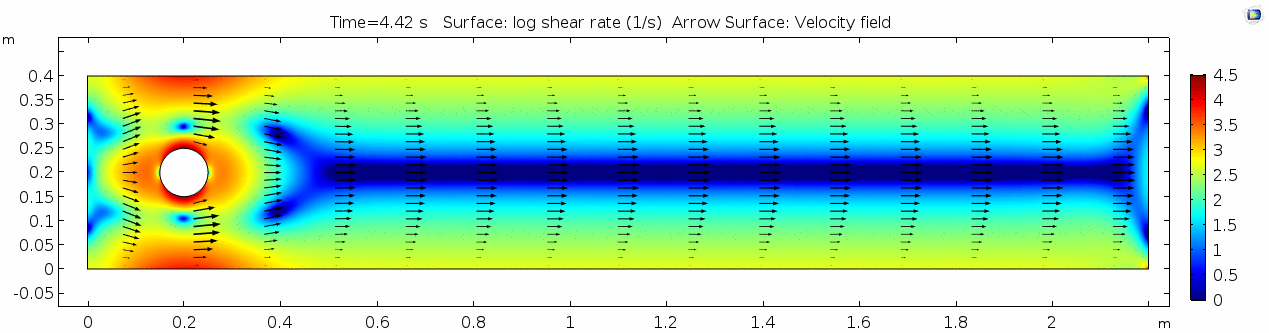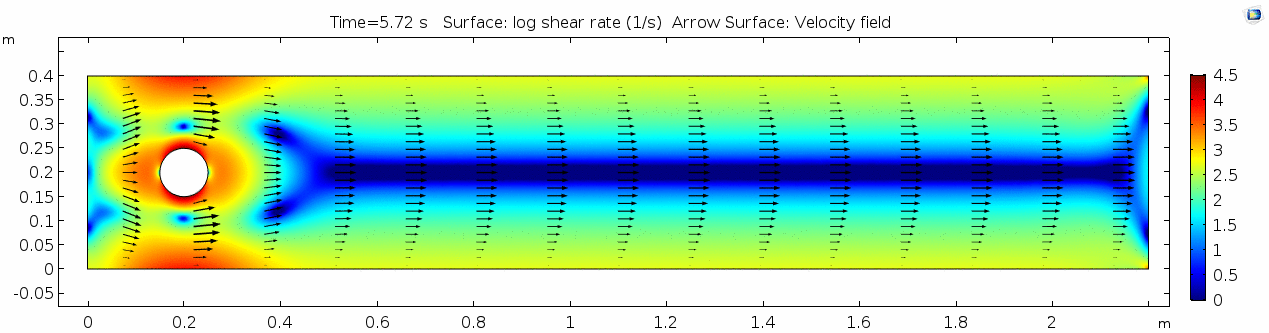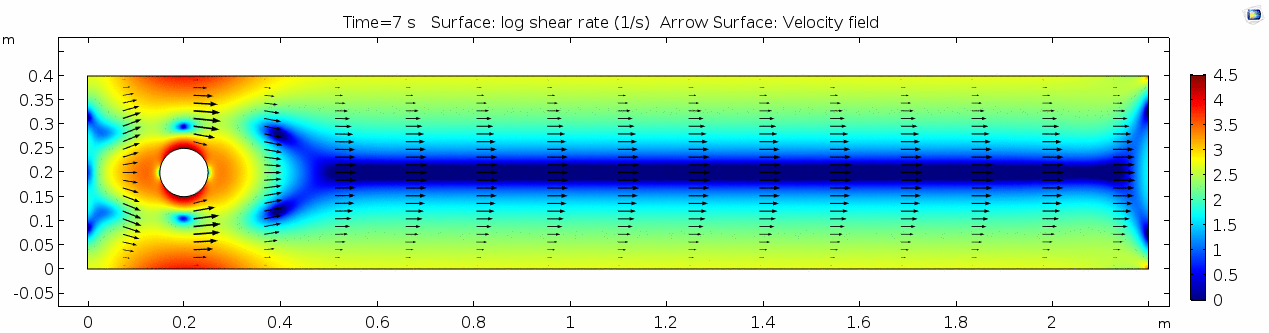
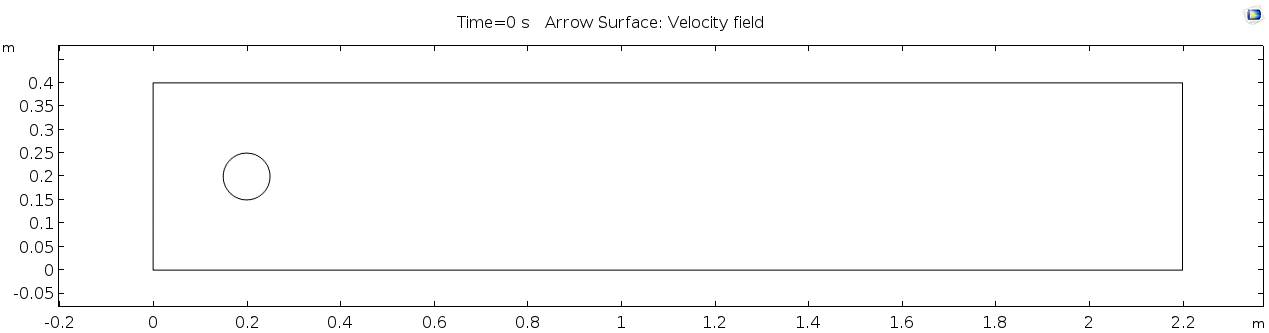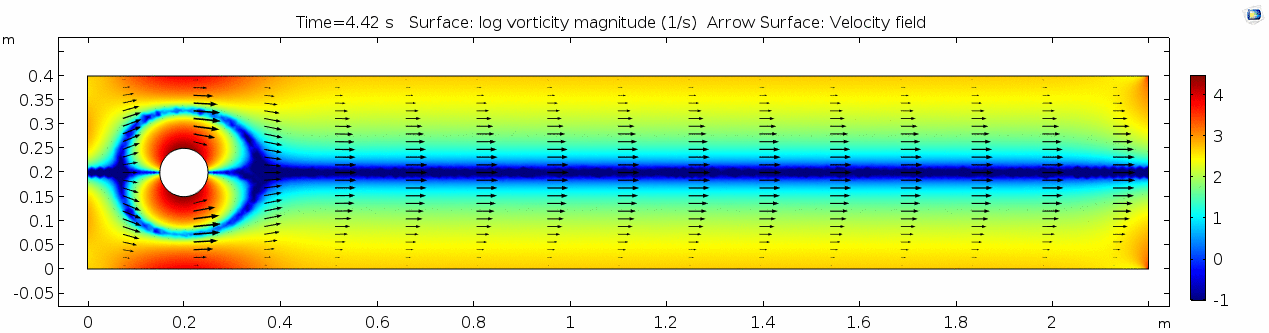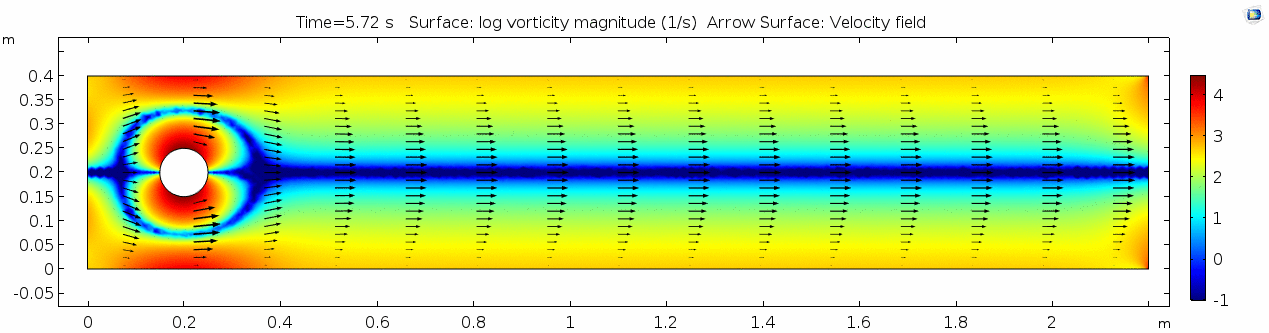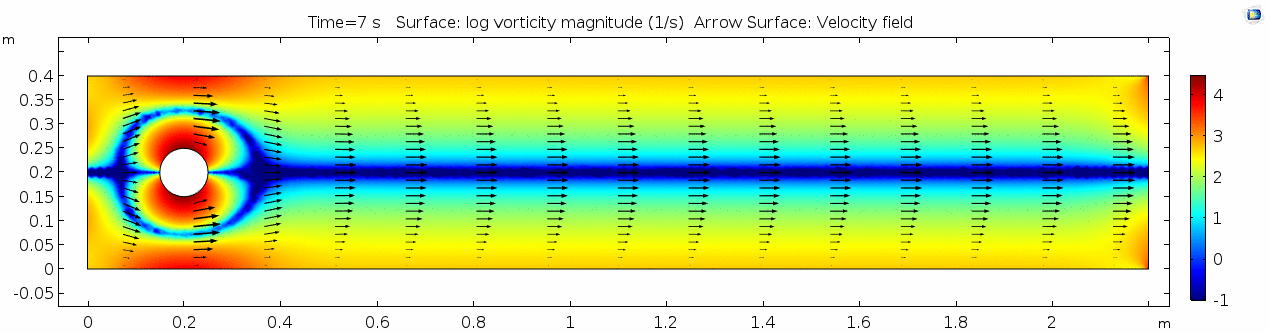
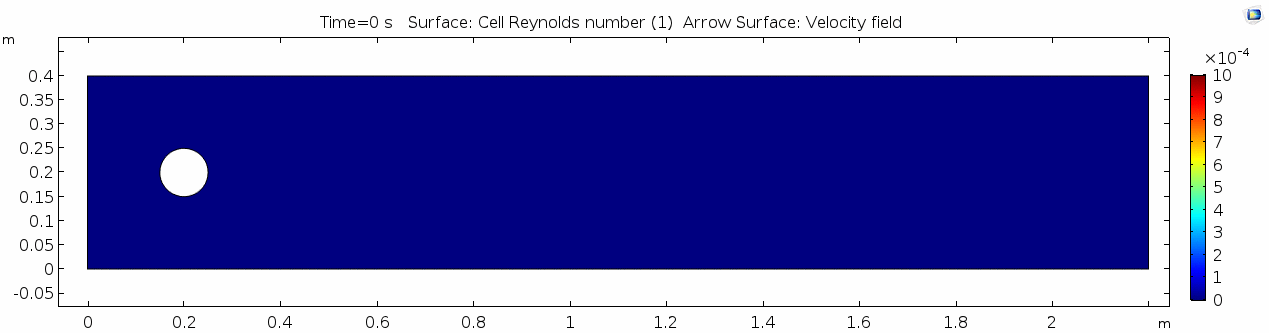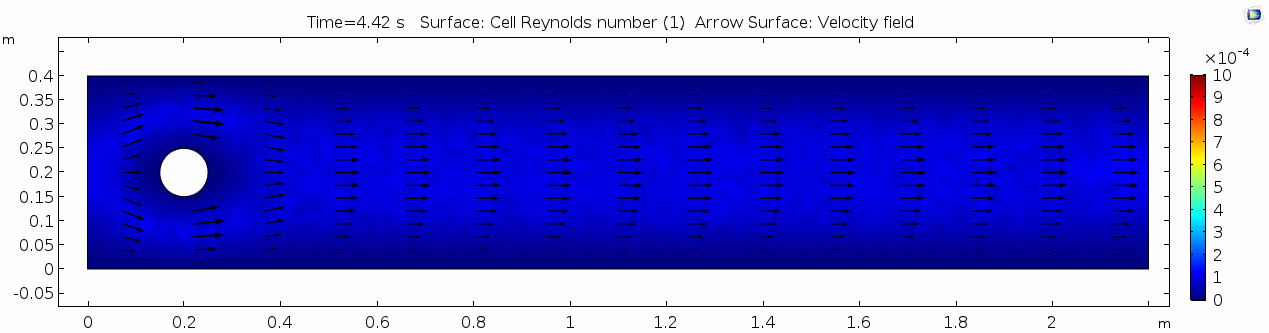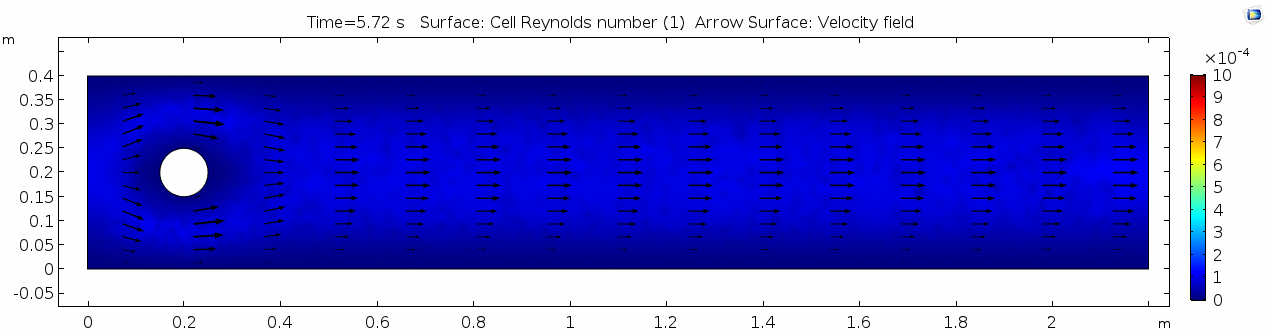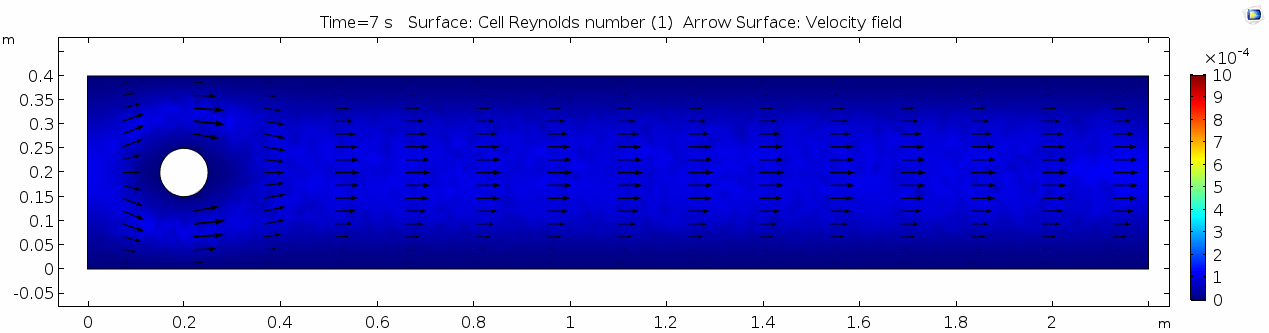
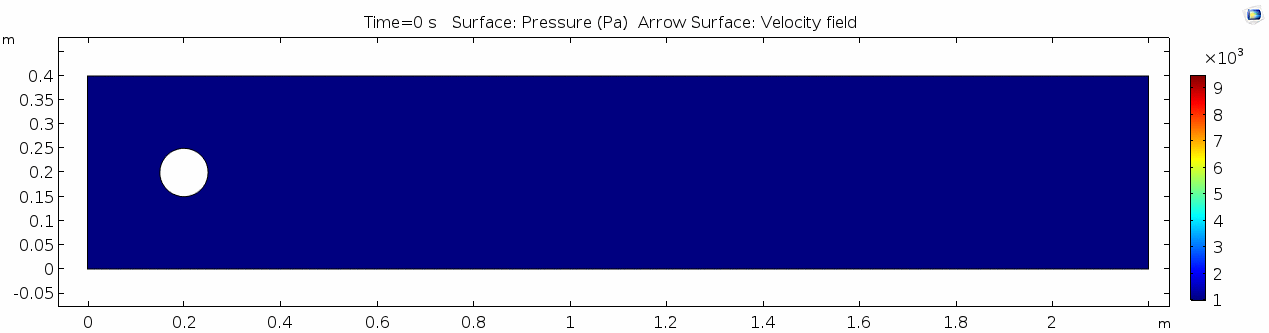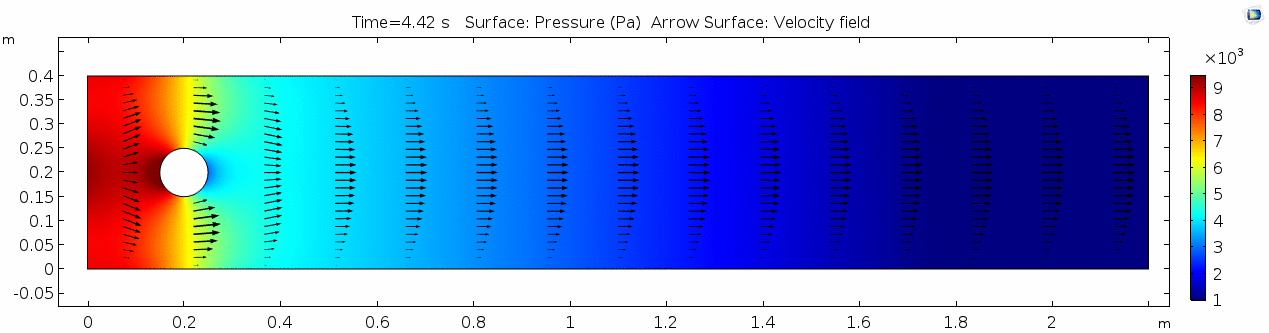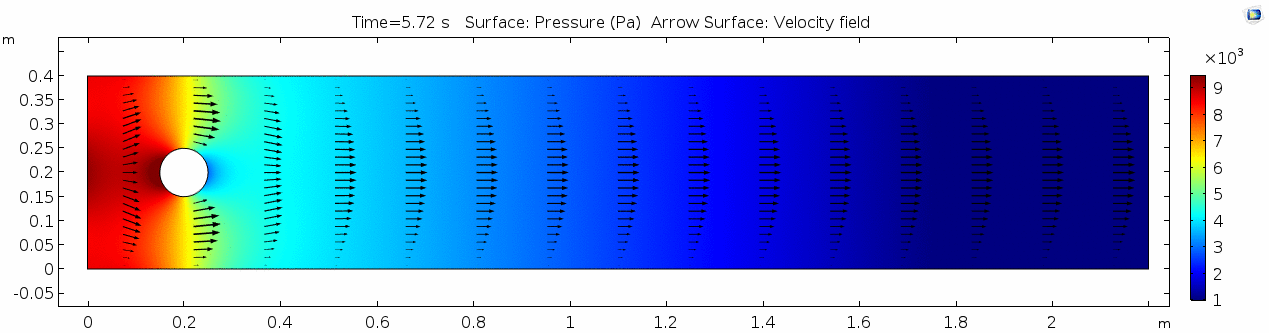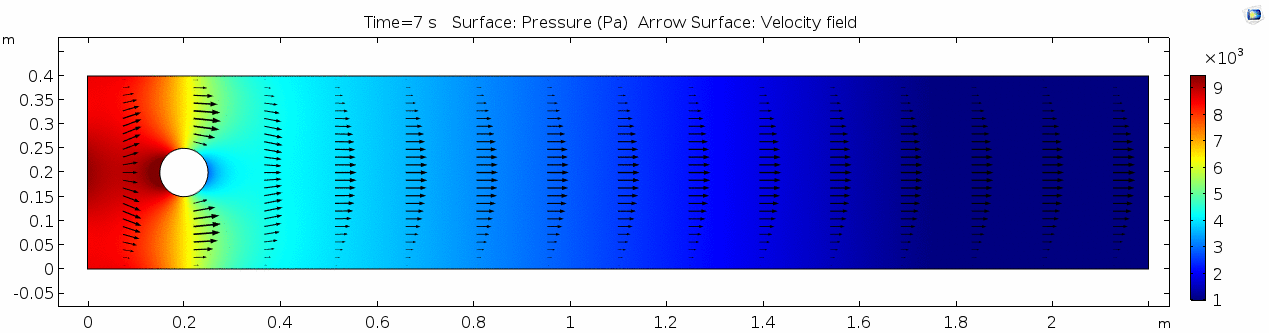
| + | In the first example, we have a fluid with the viscosity of about that of honey, 10<sup>1.5</sup> Pascal seconds (Pa s). This is a two-dimensional example, but let's assume that this model has a depth that does not affect the flow in any way. Both the horizontal walls and the walls of the cylinder on the left side of the model have a "no slip" condition. This means that as the flow gets closer to the wall, velocity goes to zero. This condition sets up a velocity gradient. | ||
| + | |||
| + | === Velocity field === | ||
| + | [[File:Mu101.5_ux1_velocity.gif]] | ||
| + | |||
| + | === Shear rate === | ||
| + | [[File:Mu101.5 ux1 shear.gif]] | ||
| + | |||
| + | === Vorticity magnitude === | ||
| + | [[File:Mu101.5 ux1 vorticity.gif]] | ||
| + | |||
| + | === Reynolds number === | ||
| + | [[File:Mu101.5 ux1 reynolds.gif]] | ||
| + | |||
| + | === Pressure === | ||
| + | [[File:Mu101.5 ux1 pressure.gif]] | ||
Revision as of 23:28, 19 February 2019
Created by Ian Nesbitt and Jukes Liu on 2019-02-19
In this module, you will learn how viscosity affects the dynamics of a simple fluid system with a single cylindrical impediment placed in the flow path. Our tools in this endeavor are COMSOL Multiphysics and ParaView. At the end of the module, you should be able to describe the initial conditions of a system, the transition from laminar to turbulent flow, and the effect viscosity has on the inertia, complexity, and predictability of a system.
We will start with a higher viscosity regime and move to lower viscosity.
First, let's start by learning how to talk about the various components of flow.
Contents
Basics
Model
Honey (μ = 101.5 Pa s)
In the first example, we have a fluid with the viscosity of about that of honey, 101.5 Pascal seconds (Pa s). This is a two-dimensional example, but let's assume that this model has a depth that does not affect the flow in any way. Both the horizontal walls and the walls of the cylinder on the left side of the model have a "no slip" condition. This means that as the flow gets closer to the wall, velocity goes to zero. This condition sets up a velocity gradient.
Velocity field
Shear rate
Vorticity magnitude
Reynolds number
Pressure