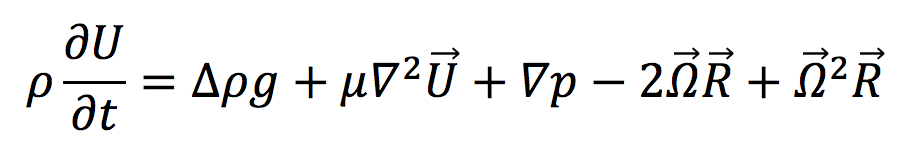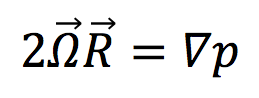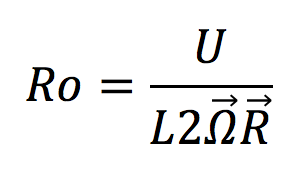Difference between revisions of "Coriolis Module"
| (13 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
| − | + | [[File:storm.png|700px|center]] | |
Today in this module we will discuss the implications of the Earth in rotation. As you are reading this, the Earth is rotating at a rate of 40,075 kilometers per day (at the equator). As we will learn, this motion will have an important effect on long distance trajectories and large-scale fluids like ocean currents and large scale atmospheric flows. | Today in this module we will discuss the implications of the Earth in rotation. As you are reading this, the Earth is rotating at a rate of 40,075 kilometers per day (at the equator). As we will learn, this motion will have an important effect on long distance trajectories and large-scale fluids like ocean currents and large scale atmospheric flows. | ||
| Line 22: | Line 22: | ||
| − | + | [[File:camera_not_mounted.jpg|300px]] [[File:mounted_camera.jpg|300px]] | |
| Line 28: | Line 28: | ||
For this video demonstration, a non-rotating reference frame is taken into consideration. Think of an astronaut in outer space, above the Earth, watching it rotating below her. | For this video demonstration, a non-rotating reference frame is taken into consideration. Think of an astronaut in outer space, above the Earth, watching it rotating below her. | ||
| − | {{#ev:youtube| | + | {{#ev:youtube|3qmprXvC5Ts}} |
| Line 68: | Line 68: | ||
Now we will look at fluids in action. The following video shows a bucket of water that spins in a rotating reference frame. At certain points in the video, color dye is added to show rotation within the fluid. | Now we will look at fluids in action. The following video shows a bucket of water that spins in a rotating reference frame. At certain points in the video, color dye is added to show rotation within the fluid. | ||
| − | {{#ev:youtube| | + | {{#ev:youtube|LxZQm4lPwkM}} |
| Line 85: | Line 85: | ||
To begin our discussion of pressure gradients, think of a bucket of honey. If the bucket is sitting flat on the floor, the surface of the honey is level, or parallel to the floor. | To begin our discussion of pressure gradients, think of a bucket of honey. If the bucket is sitting flat on the floor, the surface of the honey is level, or parallel to the floor. | ||
| − | |||
| − | |||
| − | |||
| − | |||
If you tilt the bucket, the surface of the honey will tilt. You can imagine that the honey will move so that it is parallel to the floor again. | If you tilt the bucket, the surface of the honey will tilt. You can imagine that the honey will move so that it is parallel to the floor again. | ||
| − | + | [[File:bucket1.png|300px]] [[File:bucket2.png|300px]] [[File:bucket3.png|300px]] | |
| Line 111: | Line 107: | ||
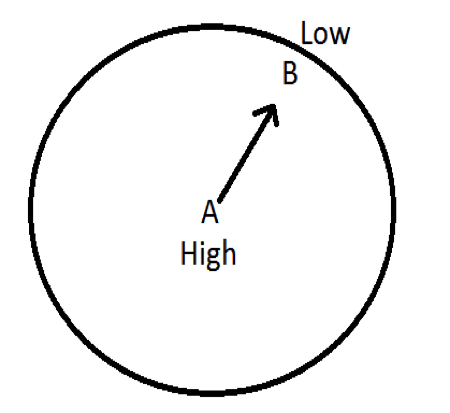
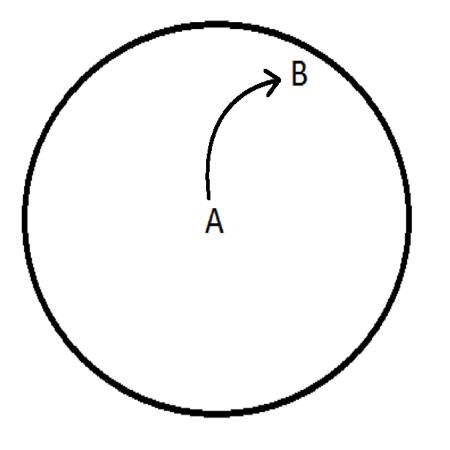
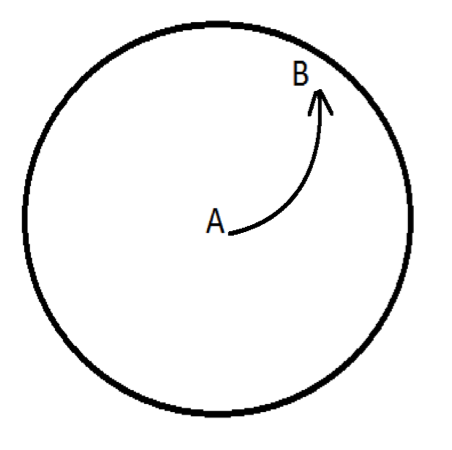
Imagine that the world is not spinning but is stationary. Draw a trajectory between high and low pressure. | Imagine that the world is not spinning but is stationary. Draw a trajectory between high and low pressure. | ||
| − | + | [[File:blank_circle.png|300px]] | |
| − | |||
| − | |||
There are two possibilities: | There are two possibilities: | ||
| − | + | [[File:circleA_B1.png|300px]] or [[File:circleAB2.png|300px]] | |
| Line 134: | Line 128: | ||
Now, pick a large vortex in the Southern Hemisphere (there are usually nice ones around Antarctica). | Now, pick a large vortex in the Southern Hemisphere (there are usually nice ones around Antarctica). | ||
Follow the same procedure as before. Does your trajectory curve differently due to Coriolis effect? Explain why this is. | Follow the same procedure as before. Does your trajectory curve differently due to Coriolis effect? Explain why this is. | ||
| + | |||
'''Answers:''' | '''Answers:''' | ||
| − | |||
| Line 158: | Line 152: | ||
| − | + | [[File:Ns_equation.png|600px]] | |
| Line 202: | Line 196: | ||
| − | + | [[File:geostrophic.png|250px]] | |
| Line 213: | Line 207: | ||
Now let’s go back to the Navier-Stokes equation: | Now let’s go back to the Navier-Stokes equation: | ||
| − | + | ||
| + | [[File:Ns_equation.png|600px]] | ||
| + | |||
Which terms drive the flow of water down your drain? Do you think the Coriolis effect influences water that drains in a sink? | Which terms drive the flow of water down your drain? Do you think the Coriolis effect influences water that drains in a sink? | ||
| Line 226: | Line 222: | ||
| − | + | [[File:rossby.png|250px]] | |
The Rossby number defines how important the Coriolis force is driving flow. If a system has a high Rossby number (the inertial force is much higher than the Coriolis force) the Coriolis force is of relatively low importance in driving flow. In this situation, the inertial force is the main driver of flow. The opposite is also true. When a system has a low Rossby number (the inertial force is much smaller than the Coriolis force), inertial force is relatively unimportant and Coriolis force is the main driver of flow. | The Rossby number defines how important the Coriolis force is driving flow. If a system has a high Rossby number (the inertial force is much higher than the Coriolis force) the Coriolis force is of relatively low importance in driving flow. In this situation, the inertial force is the main driver of flow. The opposite is also true. When a system has a low Rossby number (the inertial force is much smaller than the Coriolis force), inertial force is relatively unimportant and Coriolis force is the main driver of flow. | ||
| − | The Rossby number is key to understanding a common myth. You might have heard that sinks in the Northern Hemisphere drain in one direction, while sinks in the Southern Hemisphere drain in the other direction due to the Coriolis force. By examining the Rossby number of a draining sink, we can tell that this is not true; the Rossby number is too big. In other words, the other inertial forces are far stronger than the Coriolis force at the scale of a draining sink. The direction of the vorticity in the drain is caused by the shape of the sink and the direction that the water is | + | The Rossby number is key to understanding a common myth. You might have heard that sinks in the Northern Hemisphere drain in one direction, while sinks in the Southern Hemisphere drain in the other direction due to the Coriolis force. By examining the Rossby number of a draining sink, we can tell that this is not true; the Rossby number is too big. In other words, the other inertial forces are far stronger than the Coriolis force at the scale of a draining sink. The direction of the vorticity in the drain is caused by the shape of the sink and the direction that the water is forced in, not the rotation of the Earth. |
Latest revision as of 20:01, 30 April 2015
Today in this module we will discuss the implications of the Earth in rotation. As you are reading this, the Earth is rotating at a rate of 40,075 kilometers per day (at the equator). As we will learn, this motion will have an important effect on long distance trajectories and large-scale fluids like ocean currents and large scale atmospheric flows.
Some important terms to keep in mind:
Reference frame: a system of axes in relation to which measurements of size, position, or motion can be made. We will be discussing 2 different reference frames: rotating and non-rotating.
Trajectory: the path of an object.
To start this learning module, we will look at a spinning plate. This plate represents a 2-dimentional view of the Northern Hemisphere as if you are looking down from above the North Pole.
Model Setup
For the first section, a non-rotating reference frame, the camera is held over the spinning plate and not put into motion. As for the second section, a rotating reference frame, the camera is mounted to the spinning plate. The plate is rotated using a stable power supply and can be switched to rotate clockwise or counterclockwise.
Non-Rotating Reference Frame
For this video demonstration, a non-rotating reference frame is taken into consideration. Think of an astronaut in outer space, above the Earth, watching it rotating below her.
You try:
Draw the ball’s trajectory. Is this what you would expect? Why or why not?
Answer: As you will notice, the ball travels on a straight trajectory.
Rotating Reference Frame
Now imagine that you are standing at the North Pole (you are rotating with the earth) and you throw a ball towards the equator. If you were tall enough to see all the way to the equator, what trajectory would the ball take?
You try:
Which way does the Earth rotate?
Will the ball travel in a straight line, relative to the surface of the Earth?
If the ball curves, which way will it curve?
<insert simple trajectory picture here>
Answer:
The Earth rotates counterclockwise when looking at it from above. The ball will not travel in a straight line but will appear to curve to the right, relative to the Earth.
In the following video, the disc is rotating the same direction as before, counterclockwise. However, this time the camera rotates with it, putting the viewers in the rotating reference frame.
You will notice that the ball appears to curves to the right of its original trajectory. This is due to the Coriolis effect, the effect that causes trajectories to appear to curve when observed from within the rotating reference frame.
Coriolis and Fluids
Now we will look at fluids in action. The following video shows a bucket of water that spins in a rotating reference frame. At certain points in the video, color dye is added to show rotation within the fluid.
You should notice some swirls forming. These swirls are called vortices, but on Earth we call them storms or cyclones.
You try:
Pick out a few different vortices. Feel free to watch the video multiple times and pause it to look at the vortices. Which way are they rotating? Are they all rotating in the same direction?
Answer:
Some vortices are rotating clockwise while others are rotating counterclockwise. The fluid is actually spinning counterclockwise but not as fast as the spinning bucket. This makes the fluid appear to rotate counterclockwise. The vorticies rotating counterclockwise are called cyclonic and clockwise are called anticyclonic. The anticyclones in this video are forming mostly due to the interaction with the sides and the bottom. In truth, it is hard to formulate a model for large-scale flows inside a small lab. Within this model, there are a lot of forces at play. We will focus on the most important terms that will help explain large-scale atmospheric flows. First, we need to go over a few details.
The Pressure Gradient
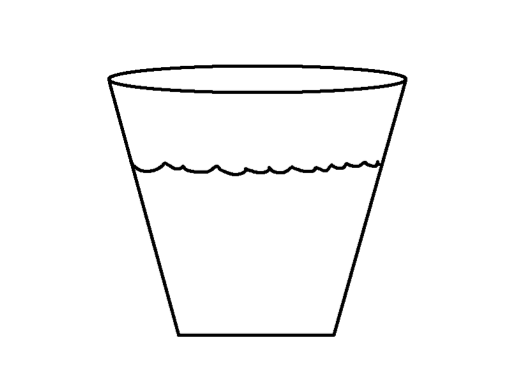
To begin our discussion of pressure gradients, think of a bucket of honey. If the bucket is sitting flat on the floor, the surface of the honey is level, or parallel to the floor.
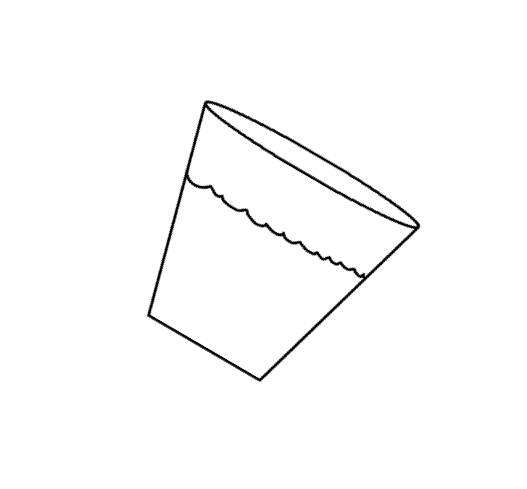
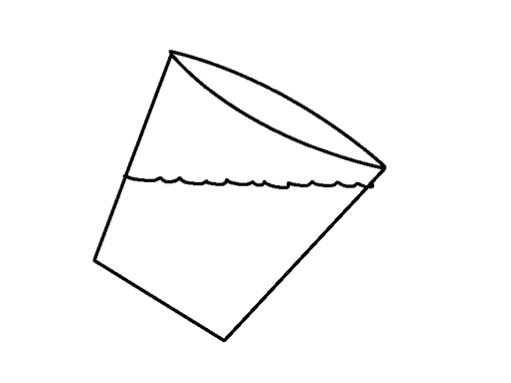
If you tilt the bucket, the surface of the honey will tilt. You can imagine that the honey will move so that it is parallel to the floor again.
When the bucket is flat on the floor, the honey has the same potential energy all the way across the bucket. When the bucket is tilted, the honey on the higher side of the bucket increases its potential energy because its height is above the lower side. The opposite is true: the honey on the lower side of the bucket has less potential energy because it is lower. The honey sloshes back to a leveled surface to find an equal amount of potential energy on all sides of the bucket. For that brief instant when the potential energy is different on the two sides of the bucket, we say there is a potential energy gradient.
In this example, where there is high potential energy, there also exists high pressure. Likewise there is low potential energy there is low pressure and fluids tend to flow from high to low pressure. This is more apparent in fluids that flow faster, like rivers.
You try: The following problems will be tested through EarthWind (link below). First we will look at a map of the mean sea level pressure.
The colors indicate high and low pressure and while the lines indicate surface wind direction. Click on the “earth” button at the bottom left to look at the color scale. The scale goes from low pressure on the left to high pressure on the right.
You try:
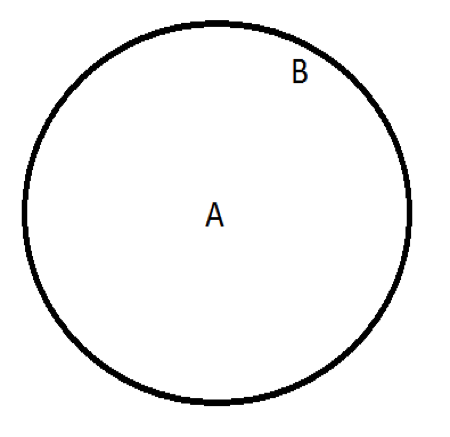
Imagine that the world is not spinning but is stationary. Draw a trajectory between high and low pressure.
There are two possibilities:
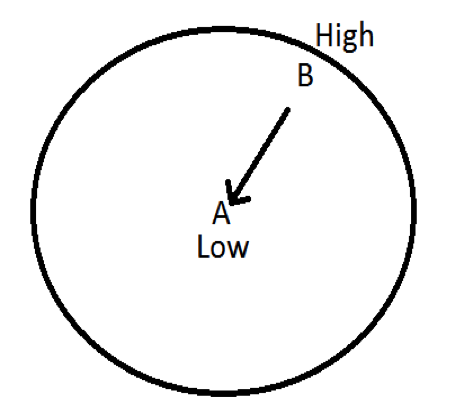
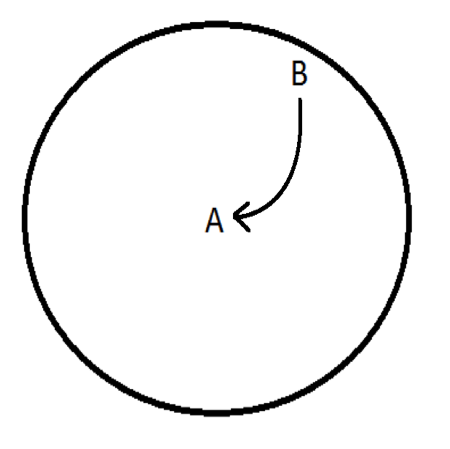
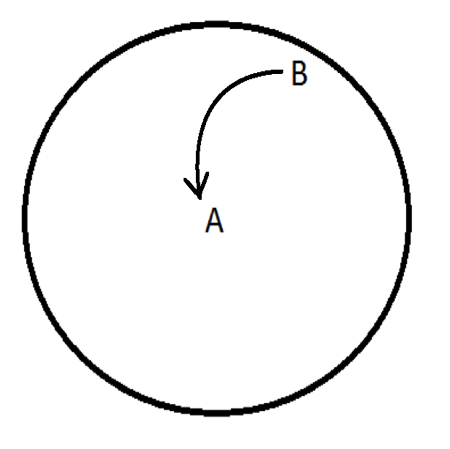
Think about what happens in a rotating reference frame. We discussed that trajectories curve right in the Northern Hemisphere due to the Coriolis effect. Draw the new curved trajectory.
Again, there are two possibilities depending on the locations of the high and low pressures:
Check your answers with EarthWind. Since wind always flows out of high pressure areas and inward in low pressure centers, wind moves clockwise around a high pressure and counterclockwise around a low pressure.
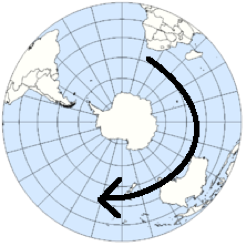
Now, pick a large vortex in the Southern Hemisphere (there are usually nice ones around Antarctica). Follow the same procedure as before. Does your trajectory curve differently due to Coriolis effect? Explain why this is.
Answers:
Imagine that you’re standing at the South Pole. From this perspective the earth appears to be rotating clockwise. Therefore, Coriolis effect causes trajectory paths to curve to the left.
In the above image, the arrow shows the rotation when viewing from above the South Pole. Now that we have described these processes qualitatively, we will move forward into a more advanced quantitative mathematical description.
Navier-Stokes Equations
The following equation mathematically represents all fluids within a rotating framework:
where…
ρ = density of the fluid
U = velocity in the x direction
t = time
g = gravity
μ = viscosity of the fluid
p = pressure
Ω = angular velocity
R = radius of rotation
The Navier-Stokes equation follows Newton’s second law, F=ma, as expressed in terms of the velocity field of a fluid as opposed to an expression for its particle paths. This equation is derived from several equations such as conservation of mass, conservation of momentum, conservation of energy, and the equation of state.
The equation quantifies that the flux of a fluid is equal to its acceleration due to gravitational flow, viscosity, frictional force, changes in pressure, the Coriolis force, and centrifugal force.
Some assumptions can be made to simplify the expression substantially. In specific applications of the Navier-Stokes equation, certain values become so small that they have very little effect on the solution. In this case it can be said that they are negligible and ignore them to make the solution more approachable.
You try: We will continue with an example of the jet stream. Click the link below,
and think about what drives its motion. Which terms do you think are important and which do you think are not important? Does the viscosity of the flow affect it? Is it affected by pressure of the air column? Be able to defend you answer to each question.
Answers:
The Navier-Stokes equation simplifies down to these two terms, the pressure gradient, and the Coriolis term. This special case is known as geostrophic flow.
Geostrophic Flow: when Coriolis effect balances out pressure gradient forces. As a result, the fluid flows along lines of equal pressure.
How about a different example? Think about the water draining down a sink. Watch these two videos that claim to show draining sink flowing differently due to the Coriolis effect in the Northern and Southern Hemispheres.
Now let’s go back to the Navier-Stokes equation:
Which terms drive the flow of water down your drain? Do you think the Coriolis effect influences water that drains in a sink?
Answer: In order to better answer this, we will discuss the Rossby Number.
Rossby number
Rossby number (Ro): the ratio of inertial forces to Coriolis force.
The Rossby number defines how important the Coriolis force is driving flow. If a system has a high Rossby number (the inertial force is much higher than the Coriolis force) the Coriolis force is of relatively low importance in driving flow. In this situation, the inertial force is the main driver of flow. The opposite is also true. When a system has a low Rossby number (the inertial force is much smaller than the Coriolis force), inertial force is relatively unimportant and Coriolis force is the main driver of flow.