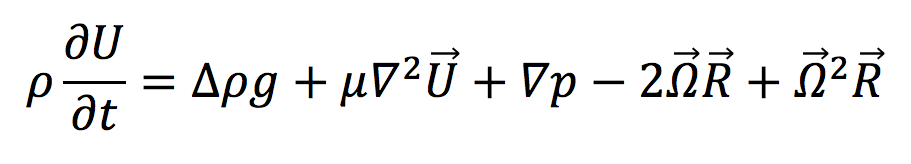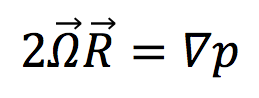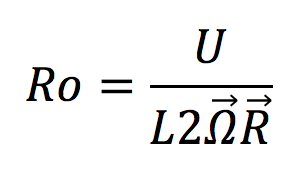Difference between revisions of "Coriolis Module"

From UMaine SECS Numerical Modeling Laboratory
Jump to: navigation, search
 
(36 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
<div style="font-size:150%">
 
<div style="font-size:150%">
−
'''Coriolis Module'''
+
 
 +
 
 +
 
 +
[[File:storm.png|700px|center]]
  
 
Today in this module we will discuss the implications of the Earth in rotation.  As you are reading this, the Earth is rotating at a rate of 40,075 kilometers per day (at the equator).  As we will learn, this motion will have an important effect on long distance trajectories and large-scale fluids like ocean currents and large scale atmospheric flows.
 
Today in this module we will discuss the implications of the Earth in rotation.  As you are reading this, the Earth is rotating at a rate of 40,075 kilometers per day (at the equator).  As we will learn, this motion will have an important effect on long distance trajectories and large-scale fluids like ocean currents and large scale atmospheric flows.
  
−
'''Some important terms to keep in mind:'''
 
  
−
''Reference frame:'' a system of axes in relation to which measurements of size, position, or motion can be made.  We will be discussing 2 different reference frames: '''rotating''' and '''non-rotating'''.
+
'''Some important terms to keep in mind:''' 
 +
 
 +
''Reference frame:'' a system of axes in relation to which measurements of size, position, or motion can be made.  We will be discussing 2 different reference frames: '''rotating''' and '''non-rotating'''.
 +
 
 +
''Trajectory'':  the path of an object.
  
−
''Trajectory'': the path of an object.
 
  
 
To start this learning module, we will look at a spinning plate.  This plate represents a 2-dimentional view of the Northern Hemisphere as if you are looking down from above the North Pole.
 
To start this learning module, we will look at a spinning plate.  This plate represents a 2-dimentional view of the Northern Hemisphere as if you are looking down from above the North Pole.
  
−
'''
+
 
−
Model Setup'''
+
'''Model Setup'''
 
For the first section, a non-rotating reference frame, the camera is held over the spinning plate and not put into motion.  As for the second section, a rotating reference frame, the camera is mounted to the spinning plate.  The plate is rotated using a stable power supply and can be switched to rotate clockwise or counterclockwise.
 
For the first section, a non-rotating reference frame, the camera is held over the spinning plate and not put into motion.  As for the second section, a rotating reference frame, the camera is mounted to the spinning plate.  The plate is rotated using a stable power supply and can be switched to rotate clockwise or counterclockwise.
  
−
<insert picture here>
+
 
−
'''
+
[[File:camera_not_mounted.jpg|300px]]          [[File:mounted_camera.jpg|300px]]
−
Non-Rotating Reference Frame'''
+
 
 +
 
 +
'''Non-Rotating Reference Frame'''
 
For this video demonstration, a non-rotating reference frame is taken into consideration.  Think of an astronaut in outer space, above the Earth, watching it rotating below her.
 
For this video demonstration, a non-rotating reference frame is taken into consideration.  Think of an astronaut in outer space, above the Earth, watching it rotating below her.
  
−
<Video one>
+
{{#ev:youtube|3qmprXvC5Ts}}
 +
 
  
−
'''You try:  
+
'''You try:'''
−
'''
 
 
Draw the ball’s trajectory.  Is this what you would expect?  Why or why not?  
 
Draw the ball’s trajectory.  Is this what you would expect?  Why or why not?  
  
  
  
−
'''Answer:'''  
+
'''Answer:'''
 
As you will notice, the ball travels on a straight trajectory.  
 
As you will notice, the ball travels on a straight trajectory.  
  
−
'''Rotating Reference Frame'''
+
 
 +
'''Rotating Reference Frame'''
 
Now imagine that you are standing at the North Pole (you are rotating with the earth) and you throw a ball towards the equator.  If you were tall enough to see all the way to the equator, what trajectory would the ball take?
 
Now imagine that you are standing at the North Pole (you are rotating with the earth) and you throw a ball towards the equator.  If you were tall enough to see all the way to the equator, what trajectory would the ball take?
  
−
'''You try:'''
+
 
 +
'''You try:'''
 
Which way does the Earth rotate?  
 
Which way does the Earth rotate?  
 
Will the ball travel in a straight line, relative to the surface of the Earth?  
 
Will the ball travel in a straight line, relative to the surface of the Earth?  
 
If the ball curves, which way will it curve?
 
If the ball curves, which way will it curve?
 +
  
 
<insert simple trajectory picture here>
 
<insert simple trajectory picture here>
  
−
'''Answer:'''  
+
 
 +
'''Answer:'''
 
The Earth rotates counterclockwise when looking at it from above.  The ball will not travel in a straight line but will appear to curve to the right, relative to the Earth.
 
The Earth rotates counterclockwise when looking at it from above.  The ball will not travel in a straight line but will appear to curve to the right, relative to the Earth.
  
 
In the following video, the disc is rotating the same direction as before, counterclockwise. However, this time the camera rotates with it, putting the viewers in the rotating reference frame.  
 
In the following video, the disc is rotating the same direction as before, counterclockwise. However, this time the camera rotates with it, putting the viewers in the rotating reference frame.  
  
−
<Video 2>
+
{{#ev:youtube|ZcATYl67EMI}}
 +
 
  
 
You will notice that the ball appears to curves to the right of its original trajectory. This is due to the Coriolis effect, the effect that causes trajectories to appear to curve when observed from within the rotating reference frame.  
 
You will notice that the ball appears to curves to the right of its original trajectory. This is due to the Coriolis effect, the effect that causes trajectories to appear to curve when observed from within the rotating reference frame.  
  
−
'''Coriolis and Fluids'''
+
 
 +
'''Coriolis and Fluids'''
 +
 
 
Now we will look at fluids in action.  The following video shows a bucket of water that spins in a rotating reference frame.  At certain points in the video, color dye is added to show rotation within the fluid.
 
Now we will look at fluids in action.  The following video shows a bucket of water that spins in a rotating reference frame.  At certain points in the video, color dye is added to show rotation within the fluid.
  
−
<Video 3>
+
{{#ev:youtube|LxZQm4lPwkM}}
 +
 
  
 
You should notice some swirls forming.  These swirls are called vortices, but on Earth we call them storms or cyclones.
 
You should notice some swirls forming.  These swirls are called vortices, but on Earth we call them storms or cyclones.
  
−
'''You try:'''
+
 
 +
'''You try:'''
 
Pick out a few different vortices. Feel free to watch the video multiple times and pause it to look at the vortices.  Which way are they rotating?  Are they all rotating in the same direction?  
 
Pick out a few different vortices. Feel free to watch the video multiple times and pause it to look at the vortices.  Which way are they rotating?  Are they all rotating in the same direction?  
  
−
'''Answer:'''  
+
 
 +
'''Answer:'''
 
Some vortices are rotating clockwise while others are rotating counterclockwise.  The fluid is actually spinning counterclockwise but not as fast as the spinning bucket.  This makes the fluid appear to rotate counterclockwise.  The vorticies rotating counterclockwise are called cyclonic and clockwise are called anticyclonic.  The anticyclones in this video are forming mostly due to the interaction with the sides and the bottom.  In truth, it is hard to formulate a model for large-scale flows inside a small lab. Within this model, there are a lot of forces at play.  We will focus on the most important terms that will help explain large-scale atmospheric flows. First, we need to go over a few details.  
 
Some vortices are rotating clockwise while others are rotating counterclockwise.  The fluid is actually spinning counterclockwise but not as fast as the spinning bucket.  This makes the fluid appear to rotate counterclockwise.  The vorticies rotating counterclockwise are called cyclonic and clockwise are called anticyclonic.  The anticyclones in this video are forming mostly due to the interaction with the sides and the bottom.  In truth, it is hard to formulate a model for large-scale flows inside a small lab. Within this model, there are a lot of forces at play.  We will focus on the most important terms that will help explain large-scale atmospheric flows. First, we need to go over a few details.  
  
  
−
'''The Pressure Gradient'''
+
'''The Pressure Gradient'''
 +
 
 
To begin our discussion of pressure gradients, think of a bucket of honey.  If the bucket is sitting flat on the floor, the surface of the honey is level, or parallel to the floor.
 
To begin our discussion of pressure gradients, think of a bucket of honey.  If the bucket is sitting flat on the floor, the surface of the honey is level, or parallel to the floor.
  
 
If you tilt the bucket, the surface of the honey will tilt.  You can imagine that the honey will move so that it is parallel to the floor again.
 
If you tilt the bucket, the surface of the honey will tilt.  You can imagine that the honey will move so that it is parallel to the floor again.
 +
 +
 +
[[File:bucket1.png|300px]]          [[File:bucket2.png|300px]]          [[File:bucket3.png|300px]]
 +
 +
 
When the bucket is flat on the floor, the honey has the same potential energy all the way across the bucket.  When the bucket is tilted, the honey on the higher side of the bucket increases its potential energy because its height is above the lower side. The opposite is true: the honey on the lower side of the bucket has less potential energy because it is lower. The honey sloshes back to a leveled surface to find an equal amount of potential energy on all sides of the bucket. For that brief instant when the potential energy is different on the two sides of the bucket, we say there is a potential energy gradient.
 
When the bucket is flat on the floor, the honey has the same potential energy all the way across the bucket.  When the bucket is tilted, the honey on the higher side of the bucket increases its potential energy because its height is above the lower side. The opposite is true: the honey on the lower side of the bucket has less potential energy because it is lower. The honey sloshes back to a leveled surface to find an equal amount of potential energy on all sides of the bucket. For that brief instant when the potential energy is different on the two sides of the bucket, we say there is a potential energy gradient.
  
 
In this example, where there is high potential energy, there also exists high pressure.  Likewise there is low potential energy there is low pressure and fluids tend to flow from high to low pressure.  This is more apparent in fluids that flow faster, like rivers.  
 
In this example, where there is high potential energy, there also exists high pressure.  Likewise there is low potential energy there is low pressure and fluids tend to flow from high to low pressure.  This is more apparent in fluids that flow faster, like rivers.  
  
−
'''
+
'''You try:'''
−
You try:'''  
 
 
The following problems will be tested through EarthWind (link below).  First we will look at a map of the mean sea level pressure.  
 
The following problems will be tested through EarthWind (link below).  First we will look at a map of the mean sea level pressure.  
  
−
[http://earth.nullschool.net/#current/wind/surface/level/overlay=mean_sea_level_pressure/orthographic]
+
[http://earth.nullschool.net/#current/wind/surface/level/overlay=mean_sea_level_pressure/orthographic|EarthWind]
  
 
The colors indicate high and low pressure and while the lines indicate surface wind direction. Click on the “earth” button at the bottom left to look at the color scale. The scale goes from low pressure on the left to high pressure on the right.
 
The colors indicate high and low pressure and while the lines indicate surface wind direction. Click on the “earth” button at the bottom left to look at the color scale. The scale goes from low pressure on the left to high pressure on the right.
  
−
'''You try:'''
+
 
 +
'''You try:'''
 
Imagine that the world is not spinning but is stationary. Draw a trajectory between high and low pressure.  
 
Imagine that the world is not spinning but is stationary. Draw a trajectory between high and low pressure.  
 +
 +
[[File:blank_circle.png|300px]]
  
  
 
There are two possibilities:
 
There are two possibilities:
  
−
  or  
+
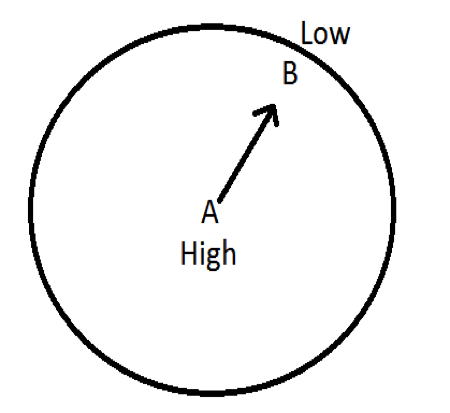
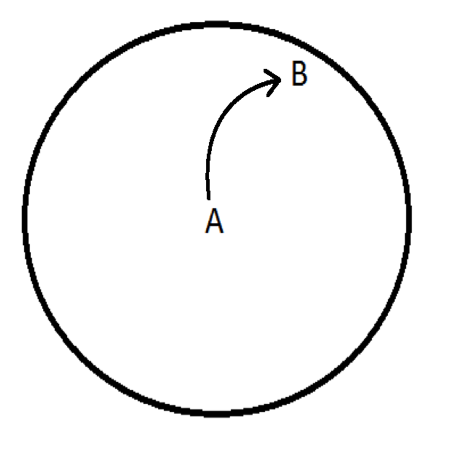
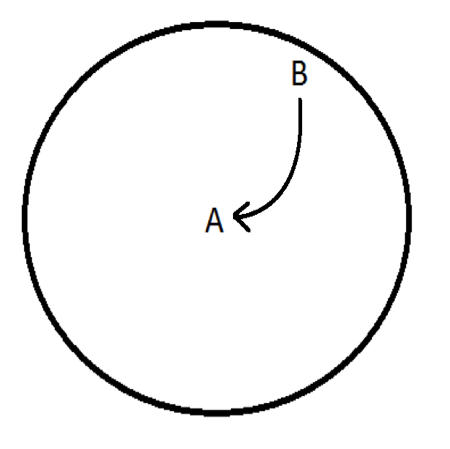
[[File:circleA_B1.png|300px]]    or     [[File:circleAB2.png|300px]]
 +
 
  
 
Think about what happens in a rotating reference frame.  We discussed that trajectories curve right in the Northern Hemisphere due to the Coriolis effect. Draw the new curved trajectory.
 
Think about what happens in a rotating reference frame.  We discussed that trajectories curve right in the Northern Hemisphere due to the Coriolis effect. Draw the new curved trajectory.
  
 
Again, there are two possibilities depending on the locations of the high and low pressures:
 
Again, there are two possibilities depending on the locations of the high and low pressures:
−
    or     
+
 
 +
 
 +
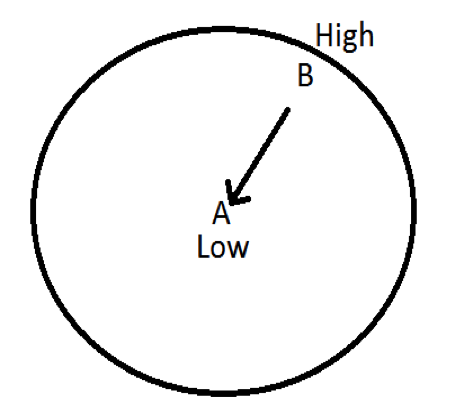
[[File:circleABcurve1.png|300px]]    or    [[File:circleABcurve2.png|300px]] 
 +
 
 +
 
  
 
Check your answers with EarthWind.  Since wind always flows out of high pressure areas and inward in low pressure centers, wind moves clockwise around a high pressure and counterclockwise around a low pressure.
 
Check your answers with EarthWind.  Since wind always flows out of high pressure areas and inward in low pressure centers, wind moves clockwise around a high pressure and counterclockwise around a low pressure.
Line 99: Line 129:
 
Follow the same procedure as before.  Does your trajectory curve differently due to Coriolis effect? Explain why this is.
 
Follow the same procedure as before.  Does your trajectory curve differently due to Coriolis effect? Explain why this is.
  
−
'''Answers:'''
 
  
−
    or     
+
'''Answers:''' 
 +
 
 +
 
 +
[[File:circleABcurve3.png|300px]]    or    [[File:circleABcurve4.png|300px]] 
 +
 
  
  
Line 108: Line 141:
  
  
−
Now that we have described these processes qualitatively, we will move forward into a more advanced quantitative mathematical description.  
+
[[File:Shemi.png|300px]]
 +
 
 +
 
 +
In the above image, the arrow shows the rotation when viewing from above the South Pole.  Now that we have described these processes qualitatively, we will move forward into a more advanced quantitative mathematical description.  
 +
 
 +
 
 +
'''Navier-Stokes Equations'''
 +
 
 +
The following equation mathematically represents all fluids within a rotating framework:
 +
 
 +
 
 +
[[File:Ns_equation.png|600px]]
 +
 
 +
 
 +
where…
 +
 
 +
ρ = density of the fluid
 +
 
 +
U = velocity in the x direction
 +
 
 +
t = time
 +
 
 +
g = gravity
  
 +
μ = viscosity of the fluid
  
 +
p = pressure
  
−
'''1. Introduction'''
+
Ω = angular velocity
  
−
Though considered to be a secondary influence behind temperature and strain rate (Billen, 2008), water does play an important role in mantle wedge rheology. Water released from a subducting oceanic lithosphere quickly saturates the mantle wedge, allows the creation of stable hydrous phases, and reduces viscosity by as much as 2 orders of magnitude (Arcay et al., 2006). The excess water that is not dissolved in the wedge continues to migrate upward into the overlying plate, where it can cause thermal erosion. I explore the effects of water on the mantle wedge through a thermal-mechanical model of Yakutat block subduction under the North American plate and use pseudosections to determine the amount of water to be released by the subducting slab. The influence on viscosity is then explored using a flow law that considers water abundance within the pre-exponential coefficient.
+
R = radius of rotation
  
  
−
'''2. Thermal-Mechanical Model''' [[File:slab_Page_1.jpg|200px|thumb|Figure 1]]
+
The ''Navier-Stokes equation'' follows Newton’s second law, F=ma, as expressed in terms of the velocity field of a fluid as opposed to an expression for its particle paths.  This equation is derived from several equations such as conservation of mass, conservation of momentum, conservation of energy, and the equation of state.  
  
−
A thermal-mechanical model is used as a 2D spatial framework for temperature and pressure that can be used to determine the expected phase assemblages within pseudosections. The model used is from Abers et al. (2006) and is meant to replicate the subduction front of the Yakutat block located beneath southern Alaska (Figure 1a). Plate geometry was attained by seismic tomography. The mantle wedge viscosity is based on a non-Newtonian dry olivine dislocation creep flow law. The mantle is coupled to the subducting and overriding slabs except within the wedge nose, where a mechanically brittle mantle is host to localized frictional sliding between plate and wedge. The geothermal gradient and advective heat transfer from wedge flow control thermal gradients within the subduction zone, and 17 mW m-2 of heat generation comes from shear heating along the fault (Figure 1b). Plate velocity is 55 mm a-1 (Nuvel-1A). The oceanic crust is 16 km thick.
+
The equation quantifies that the flux of a fluid is equal to its acceleration due to gravitational flow, viscosity, frictional force, changes in pressure, the Coriolis force, and centrifugal force.
  
 +
Some assumptions can be made to simplify the expression substantially.  In specific applications of the ''Navier-Stokes equation'', certain values become so small that they have very little effect on the solution.  In this case it can be said that they are negligible and ignore them to make the solution more approachable.
  
−
'''3. H2O saturated MORB Phase Assemblage Analysis''' [[File:slab_Page_2.jpg|200px|thumb|left|Table 1]] [[File:slab_Page_3.jpg|400px|thumb|Figure 2]]
 
  
−
I use an average bulk rock composition for north Pacific MORB from Melson et al. (1976) as a surrogate for Yakutat plate composition (Table 1). MORB compositions typically do not vary except for REE abundances which would not affect this study. The subducting MORB can experience large pressure and temperature ranges. The oceanic plate is host to excessive hydrothermal advection at the rift zone in addition to water percolation into normal faults that form by crustal bending at the trench and is therefore considered to be saturated in H2O when it subducts (Schmidt and Poli, 1998; Arcay et al., 2005).
 
−
Bulk rock composition data is used to determine phase stability in Perple_X, a thermodynamic calculation program, to determine which phases have the lowest Gibbs free energy within a specified temperature and pressure range (Connolly, 2009). I used the hp04ver.dat database file (Holland and Powell, 1998) and the solut09.dat solution model file to create pressure versus temperature pseudosections for both MORB and mantle compositions. Considered solution models for the MORB composition are listed in Table 2 and the resulting pseudosections are shown in Figure 2a-c.
 
−
Water is held in the rock’s crystal structure until lawsonite is reacted out at higher T and P, but the release of water is gradual, as seen by the red contours (Figure 2a). Lawsonite (Figure 2b) holds about 11.5 wt% water at ultrahigh pressures and can make up to 33 wt% of the entire rock at relatively high pressure and low temperature, therefore it is an important factor in mantle wedge hydration and its abundance controls H2O abundance at high pressure (Pawley and Holloway, 1993). Lawsonite abundance decreases with increasing temperature until it is completely reacted out to form eclogite facies rock. Dehydration and compression also increases the plate’s negative buoyancy (Figure 2c).
 
−
Figure 2d displays the same pseudosection but with PT paths for three positions (top, middle, and base) in the MORB crust. The starting position of the arrows is dependent on pressure at depth and temperature in the steady-state oceanic crust geothermal gradient. Plate subduction leads to a reversal of the geothermal gradient by rapid thermal advection from wedge flow into the top of the subducting slab. The plate passes through greenschist, amphibolite, blueschist, and finally eclogite facies when all water is dehydrated, and the stable phase assemblages are typical for the basaltic rendition of these facies (Schmidt and Poli, 1998). The top of the MORB crust quickly dehydrates at ~30 kbar and releases 4.55 wt% H2O, as does the center of the plate at ~50 kbar (Figure 2e). The base of the MORB crust dehydrates at ~68 kbar, but releases only 2 wt% H2O due to its initially hotter temperature. Water is released from the subducting slab continuously until the depth of 200 km (~68 kbar).
 
  
 +
'''You try:''' 
 +
We will continue with an example of the jet stream.  Click the link below,
  
 +
[http://earth.nullschool.net/#current/wind/isobaric/250hPa/overlay=mean_sea_level_pressure/orthographic=-69.69,24.13,303]
  
−
[[File:slab_Page_4.jpg|300px|thumb|left|Figure 3]] '''4. H2O Saturated Subducting Mantle Phase Assemblage Analysis'''
+
and think about what drives its motion. Which terms do you think are important and which do you think are not important?  Does the viscosity of the flow affect it?  Is it affected by pressure of the air column?  Be able to defend you answer to each question.  
  
−
Figure 3 displays the pseudosection for a saturated mantle composition (Hoffman, 1988). I also consider the subducting mantle to be saturated due to hydrothermal advection at the rift zone. There is a thin (~1km) layer of mantle lying right below the MORB crust that contains ~60 wt% Serpentinite, holding ~8.5 wt% H2O. Although thin, this layer holds a very large proportion of the subducting slab water budget, and the chemical discontinuituy between MORB and serpentinized mantle can lead to decoupling in some situations (Billen, 2008). Amphibole is stable within deeper parts of the mantle but it holds only miniscule amounts of water. Both the 1km thick serpentinized mantle layer and the 16km thick MORB crust contain a total average of 4.96 wt% H2O that can be released into the upper mantle.
 
  
 +
'''Answers:''' 
 +
The Navier-Stokes equation simplifies down to these two terms, the pressure gradient, and the Coriolis term.  This special case is known as '''geostrophic''' flow. 
  
−
'''5. H2O Limited Mantle Wedge Phase Assemblage Analysis''' [[File:slab_Page_5.jpg|400px|thumb|Figure 4]]
+
''Geostrophic Flow'': when Coriolis effect balances out pressure gradient forces.  As a result, the fluid flows along lines of equal pressure.
  
−
The water content (Table 1) used to create the mantle wedge pseudosection (Figure 4a) is limited to the amount of water that is released by lawsonite and serpentinite dehydration in the subducting slab (4.96 wt%). The blue line of Figure 4a represents the transition from all water utilized in hydrous phase assemblages to a water saturated system that requires less water. Serpentinite is restricted to a maximum of 29.46 wt% (rather than the maximum 60 wt% for a saturated mantle) within the blue range due to the limited amount of water within the wedge. The cold wedge nose also contains chlorite and amphibole (Figure 4b), and is the only location within the wedge where water is held in the crystal structure (Figure 4c). All water that is released under the wedge is taken into hydrous phases, therefore no excess water remains in the wedge nose. The red line represents the last dehydration reactions before a completely anhydrous mineral assemblage becomes stable. The only water that can exist within the rock beyond this point is dissolved water locked within olivine, cpx, opx, or garnet, and is limited to 0.146 wt% (Arcay et al., 2005; 2006).
 
  
 +
[[File:geostrophic.png|250px]]
  
−
[[File:slab_Page_6.jpg|250px|thumb|left|Figure 5]] '''6. H2O Effects on Viscosity'''
 
  
−
Mantle viscosity is reduced by the introduction of water according to the viscosity equation of Figure 5. The equation takes into account the weakening factor of hydration through the pre-exponential coefficient. The weakening factor controls the drop in viscosity through a given weight percent of water. Although temperature and strain rate are the major components that control viscosity, water can alter viscosity values by 1 order of magnitude if dissolved water is present, or 2 orders of magnitude if water is able to enter the crystal structure of a hydrous mineral (e.g., Arcay et al., 2005; 2006). All hydrous minerals exist at low temperatures, therefore their reduction in viscosity is negligible because their viscosity value is already several orders of magnitude larger. Water enhances transportability of ions and reduces cohesion between grains, allowing for more efficient diffusion and dislocation creep mechanisms under constant strain (Arcay et al., 2006; Manea and Gurnis, 2007). This contrasts with the non-Newtonian dry olivine dislocation creep flow law used in the Arcay et al. (2005) model, therefore the thermal gradients produced therein would be altered in a wet wedge system.
+
How about a different example?  Think about the water draining down a sink. Watch these two videos that claim to show draining sink flowing differently due to the Coriolis effect in the Northern and Southern Hemispheres.
−
Additionally, hydration leads to a reduced solidus for mantle compositions and can lead to melt which further reduces wedge viscosity. Melt can occur within the wedge where temperatures are highest, but reduced wedge viscosity will enhance thermal advection into the now hydrous overlying plate and initiate low viscosity mechanics and melting there as well (Billen, 2008).
 
  
 +
[https://www.youtube.com/watch?v=TGowx6w_KGk]
  
 +
[https://www.youtube.com/watch?v=HcNOcJakNW8]
  
−
'''7. Concluding Remarks'''
+
Now let’s go back to the Navier-Stokes equation:
  
−
Water should be expected in abundance within all subduction zones, and it has large effects on mantle wedge mineralogy and rheology. Water is released predominantly by dehydration of lawsonite in the MORB crust and serpentinite in the upper layer of the subducting mantle. Hydration allows growth of serpentinite and other hydrous minerals in the wedge nose, which leads to flow decoupling between the wedge and the subducting plate. Dehydration of the subducting slab leads to seismisity at greater depths (Abers et al., 2005). H2O dissolution in the anhydrous mantle wedge mineral assemblage can reduce viscosity by 1-2 orders of magnitude on top of the enhanced ability to advect heat more rapidly. Finally, excess water not taken into the wedge, which is substantial, is driven upward into the overlying plate, leading to thermal erosion and melting at its base, which will lead to volcanism and extension of the backarc.
 
−
</div>
 
  
−
'''8. Bibliography'''
+
[[File:Ns_equation.png|600px]]
  
−
Abers, G.; van Keken, P; Kneller, E.; Ferris, A.; Stachnik, J. (2006). The thermal structure of subduction zones constrained by seismic imaging: implications for slab dehydration and wedge flow. Earth and Planetary Science letters 241: 387-397.
 
  
−
Arcay, D; Doin, M.; Tric, E.; Bousquet, R.; de Capitani, C. (2006). Overriding plate thinning in subduction zones: localized convection induced by slab dehydration. Geochemistry, Geophysics, Geosystems 7.2.
+
Which terms drive the flow of water down your drain?  Do you think the Coriolis effect influences water that drains in a sink?
  
−
Arcay, D.; Tric, E.; Doin, M. (2005). Numerical simulations of subduction zones effect of slab dehydration on the mantle wedge dynamics. Physics of the Earth and Planetary Interiors 149: 133-153.
+
'''Answer:''' 
 +
In order to better answer this, we will discuss the Rossby Number.
  
−
Billen, M.I. (2008). Modeling the dynamics of subducting slabs. Annual Reviews of Earth and Planetary Sciences 36: 325-356.
 
  
−
Connolly, J. A. D. (2009) The geodynamic equation of state: what and how. Geochemistry, Geophysics, Geosystems 10:Q10014 DOI:10.1029/2009GC002540.
+
'''Rossby number'''
  
−
Hoffman, P. (1988). Archean oceanic flake tectonics. Geophysical Research Letters 15.10: 1077-1080.
+
''Rossby number (Ro):'' the ratio of inertial forces to Coriolis force.
  
−
Holland, T. J. B., & Powell, R. (1998) An internally consistent thermodynamic data set for phases of petrological interest. Journal of Metamorphic Geology 16:309-343.
 
  
−
Manea, V. and Gurnis, M. (2007). Subduction zone evolution and low viscosity wedges and channels. Earth and Planetary Science Letters 264: 22-45.
+
[[File:rossby.png|250px]]
  
−
Melson, W.; Vallier, T.; Wright, T.; Byerly, G.; Nelen, J. (1976). Chemical diversity of abyssal volcanic glass erupted along the Pacific, Atlantic, and Indian ocean seafloor spreading centers. In the Geophysics of the Pacific Ocean Basin, Geophysical Monograph series, Washington (AGU) 14: 351-368.
 
  
−
Pawley, A. and Holloway, J. (1993). Water sources for subduction zone volcanism: new experimental constraints. Science 260.5108: 664-667.
+
The Rossby number defines how important the Coriolis force is driving flow. If a system has a high Rossby number (the inertial force is much higher than the Coriolis force) the Coriolis force is of relatively low importance in driving flow. In this situation, the inertial force is the main driver of flow. The opposite is also true. When a system has a low Rossby number (the inertial force is much smaller than the Coriolis force), inertial force is relatively unimportant and Coriolis force is the main driver of flow.
  
−
Schmidt, M. and Poli, S. (1998). Experimentally based water budgets for dehydrating slabs and consequences for arc magma generation. Earth and Planetary Science Letters 163: 361-379.
+
The Rossby number is key to understanding a common myth.  You might have heard that sinks in the Northern Hemisphere drain in one direction, while sinks in the Southern Hemisphere drain in the other direction due to the Coriolis force. By examining the Rossby number of a draining sink, we can tell that this is not true; the Rossby number is too big. In other words, the other inertial forces are far stronger than the Coriolis force at the scale of a draining sink. The direction of the vorticity in the drain is caused by the shape of the sink and the direction that the water is forced in, not the rotation of the Earth.

Latest revision as of 20:01, 30 April 2015


Storm.png

Today in this module we will discuss the implications of the Earth in rotation. As you are reading this, the Earth is rotating at a rate of 40,075 kilometers per day (at the equator). As we will learn, this motion will have an important effect on long distance trajectories and large-scale fluids like ocean currents and large scale atmospheric flows.


Some important terms to keep in mind:

Reference frame: a system of axes in relation to which measurements of size, position, or motion can be made. We will be discussing 2 different reference frames: rotating and non-rotating.

Trajectory: the path of an object.


To start this learning module, we will look at a spinning plate. This plate represents a 2-dimentional view of the Northern Hemisphere as if you are looking down from above the North Pole.


Model Setup For the first section, a non-rotating reference frame, the camera is held over the spinning plate and not put into motion. As for the second section, a rotating reference frame, the camera is mounted to the spinning plate. The plate is rotated using a stable power supply and can be switched to rotate clockwise or counterclockwise.


Camera not mounted.jpg Mounted camera.jpg


Non-Rotating Reference Frame For this video demonstration, a non-rotating reference frame is taken into consideration. Think of an astronaut in outer space, above the Earth, watching it rotating below her.


You try: Draw the ball’s trajectory. Is this what you would expect? Why or why not?


Answer: As you will notice, the ball travels on a straight trajectory.


Rotating Reference Frame Now imagine that you are standing at the North Pole (you are rotating with the earth) and you throw a ball towards the equator. If you were tall enough to see all the way to the equator, what trajectory would the ball take?


You try: Which way does the Earth rotate? Will the ball travel in a straight line, relative to the surface of the Earth? If the ball curves, which way will it curve?


<insert simple trajectory picture here>


Answer: The Earth rotates counterclockwise when looking at it from above. The ball will not travel in a straight line but will appear to curve to the right, relative to the Earth.

In the following video, the disc is rotating the same direction as before, counterclockwise. However, this time the camera rotates with it, putting the viewers in the rotating reference frame.


You will notice that the ball appears to curves to the right of its original trajectory. This is due to the Coriolis effect, the effect that causes trajectories to appear to curve when observed from within the rotating reference frame.


Coriolis and Fluids

Now we will look at fluids in action. The following video shows a bucket of water that spins in a rotating reference frame. At certain points in the video, color dye is added to show rotation within the fluid.


You should notice some swirls forming. These swirls are called vortices, but on Earth we call them storms or cyclones.


You try: Pick out a few different vortices. Feel free to watch the video multiple times and pause it to look at the vortices. Which way are they rotating? Are they all rotating in the same direction?


Answer: Some vortices are rotating clockwise while others are rotating counterclockwise. The fluid is actually spinning counterclockwise but not as fast as the spinning bucket. This makes the fluid appear to rotate counterclockwise. The vorticies rotating counterclockwise are called cyclonic and clockwise are called anticyclonic. The anticyclones in this video are forming mostly due to the interaction with the sides and the bottom. In truth, it is hard to formulate a model for large-scale flows inside a small lab. Within this model, there are a lot of forces at play. We will focus on the most important terms that will help explain large-scale atmospheric flows. First, we need to go over a few details.


The Pressure Gradient

To begin our discussion of pressure gradients, think of a bucket of honey. If the bucket is sitting flat on the floor, the surface of the honey is level, or parallel to the floor.

If you tilt the bucket, the surface of the honey will tilt. You can imagine that the honey will move so that it is parallel to the floor again.


Bucket1.png Bucket2.png Bucket3.png


When the bucket is flat on the floor, the honey has the same potential energy all the way across the bucket. When the bucket is tilted, the honey on the higher side of the bucket increases its potential energy because its height is above the lower side. The opposite is true: the honey on the lower side of the bucket has less potential energy because it is lower. The honey sloshes back to a leveled surface to find an equal amount of potential energy on all sides of the bucket. For that brief instant when the potential energy is different on the two sides of the bucket, we say there is a potential energy gradient.

In this example, where there is high potential energy, there also exists high pressure. Likewise there is low potential energy there is low pressure and fluids tend to flow from high to low pressure. This is more apparent in fluids that flow faster, like rivers.

You try: The following problems will be tested through EarthWind (link below). First we will look at a map of the mean sea level pressure.

[1]

The colors indicate high and low pressure and while the lines indicate surface wind direction. Click on the “earth” button at the bottom left to look at the color scale. The scale goes from low pressure on the left to high pressure on the right.


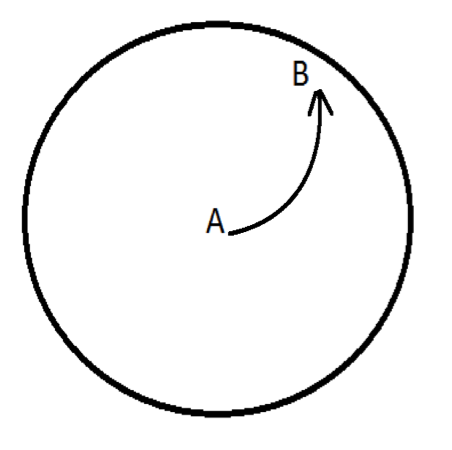
You try: Imagine that the world is not spinning but is stationary. Draw a trajectory between high and low pressure.

Blank circle.png


There are two possibilities:

CircleA B1.png or CircleAB2.png


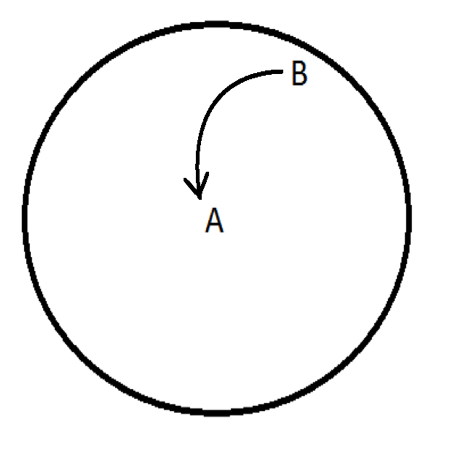
Think about what happens in a rotating reference frame. We discussed that trajectories curve right in the Northern Hemisphere due to the Coriolis effect. Draw the new curved trajectory.

Again, there are two possibilities depending on the locations of the high and low pressures:


CircleABcurve1.png or CircleABcurve2.png


Check your answers with EarthWind. Since wind always flows out of high pressure areas and inward in low pressure centers, wind moves clockwise around a high pressure and counterclockwise around a low pressure.

Now, pick a large vortex in the Southern Hemisphere (there are usually nice ones around Antarctica). Follow the same procedure as before. Does your trajectory curve differently due to Coriolis effect? Explain why this is.


Answers:


CircleABcurve3.png or CircleABcurve4.png


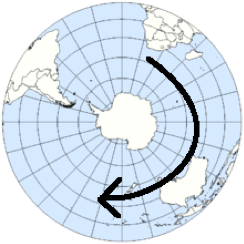
Imagine that you’re standing at the South Pole. From this perspective the earth appears to be rotating clockwise. Therefore, Coriolis effect causes trajectory paths to curve to the left.


Shemi.png


In the above image, the arrow shows the rotation when viewing from above the South Pole. Now that we have described these processes qualitatively, we will move forward into a more advanced quantitative mathematical description.


Navier-Stokes Equations

The following equation mathematically represents all fluids within a rotating framework:


Ns equation.png


where…

ρ = density of the fluid

U = velocity in the x direction

t = time

g = gravity

μ = viscosity of the fluid

p = pressure

Ω = angular velocity

R = radius of rotation


The Navier-Stokes equation follows Newton’s second law, F=ma, as expressed in terms of the velocity field of a fluid as opposed to an expression for its particle paths. This equation is derived from several equations such as conservation of mass, conservation of momentum, conservation of energy, and the equation of state.

The equation quantifies that the flux of a fluid is equal to its acceleration due to gravitational flow, viscosity, frictional force, changes in pressure, the Coriolis force, and centrifugal force.

Some assumptions can be made to simplify the expression substantially. In specific applications of the Navier-Stokes equation, certain values become so small that they have very little effect on the solution. In this case it can be said that they are negligible and ignore them to make the solution more approachable.


You try: We will continue with an example of the jet stream. Click the link below,

[2]

and think about what drives its motion. Which terms do you think are important and which do you think are not important? Does the viscosity of the flow affect it? Is it affected by pressure of the air column? Be able to defend you answer to each question.


Answers: The Navier-Stokes equation simplifies down to these two terms, the pressure gradient, and the Coriolis term. This special case is known as geostrophic flow.

Geostrophic Flow: when Coriolis effect balances out pressure gradient forces. As a result, the fluid flows along lines of equal pressure.


Geostrophic.png


How about a different example? Think about the water draining down a sink. Watch these two videos that claim to show draining sink flowing differently due to the Coriolis effect in the Northern and Southern Hemispheres.

[3]

[4]

Now let’s go back to the Navier-Stokes equation:


Ns equation.png


Which terms drive the flow of water down your drain? Do you think the Coriolis effect influences water that drains in a sink?

Answer: In order to better answer this, we will discuss the Rossby Number.


Rossby number

Rossby number (Ro): the ratio of inertial forces to Coriolis force.


Rossby.png


The Rossby number defines how important the Coriolis force is driving flow. If a system has a high Rossby number (the inertial force is much higher than the Coriolis force) the Coriolis force is of relatively low importance in driving flow. In this situation, the inertial force is the main driver of flow. The opposite is also true. When a system has a low Rossby number (the inertial force is much smaller than the Coriolis force), inertial force is relatively unimportant and Coriolis force is the main driver of flow.

The Rossby number is key to understanding a common myth. You might have heard that sinks in the Northern Hemisphere drain in one direction, while sinks in the Southern Hemisphere drain in the other direction due to the Coriolis force. By examining the Rossby number of a draining sink, we can tell that this is not true; the Rossby number is too big. In other words, the other inertial forces are far stronger than the Coriolis force at the scale of a draining sink. The direction of the vorticity in the drain is caused by the shape of the sink and the direction that the water is forced in, not the rotation of the Earth.
Retrieved from "http://wiki.geodynamics.umaine.edu/index.php?title=Coriolis_Module&oldid=582"