Difference between revisions of "Strain Partitioning and Fault Segmentation"
| Line 46: | Line 46: | ||
! style="width:330px" | Fault segments defined as friction angles (blue: fault, red: bedrock) | ! style="width:330px" | Fault segments defined as friction angles (blue: fault, red: bedrock) | ||
|- | |- | ||
| − | | | + | | {{#ev:youtube|https://www.youtube.com/watch?v=3-_huWk-BFU|700px}} |
| − | | | + | | {{#ev:youtube|https://www.youtube.com/watch?v=mWvKUxMVpjQ|700px}} |
|} | |} | ||
Latest revision as of 17:12, 12 June 2018
Role of topography, rock rheology, and boundary conditions in strain partitioning and fault evolution in active transpressional orogens
Song, B.R. 1; Upton, P. 1, 2; Koons, P.O. 1
- 1 School of Earth and Climate Sciences, University of Maine
- 2 GNS Science
Introduction
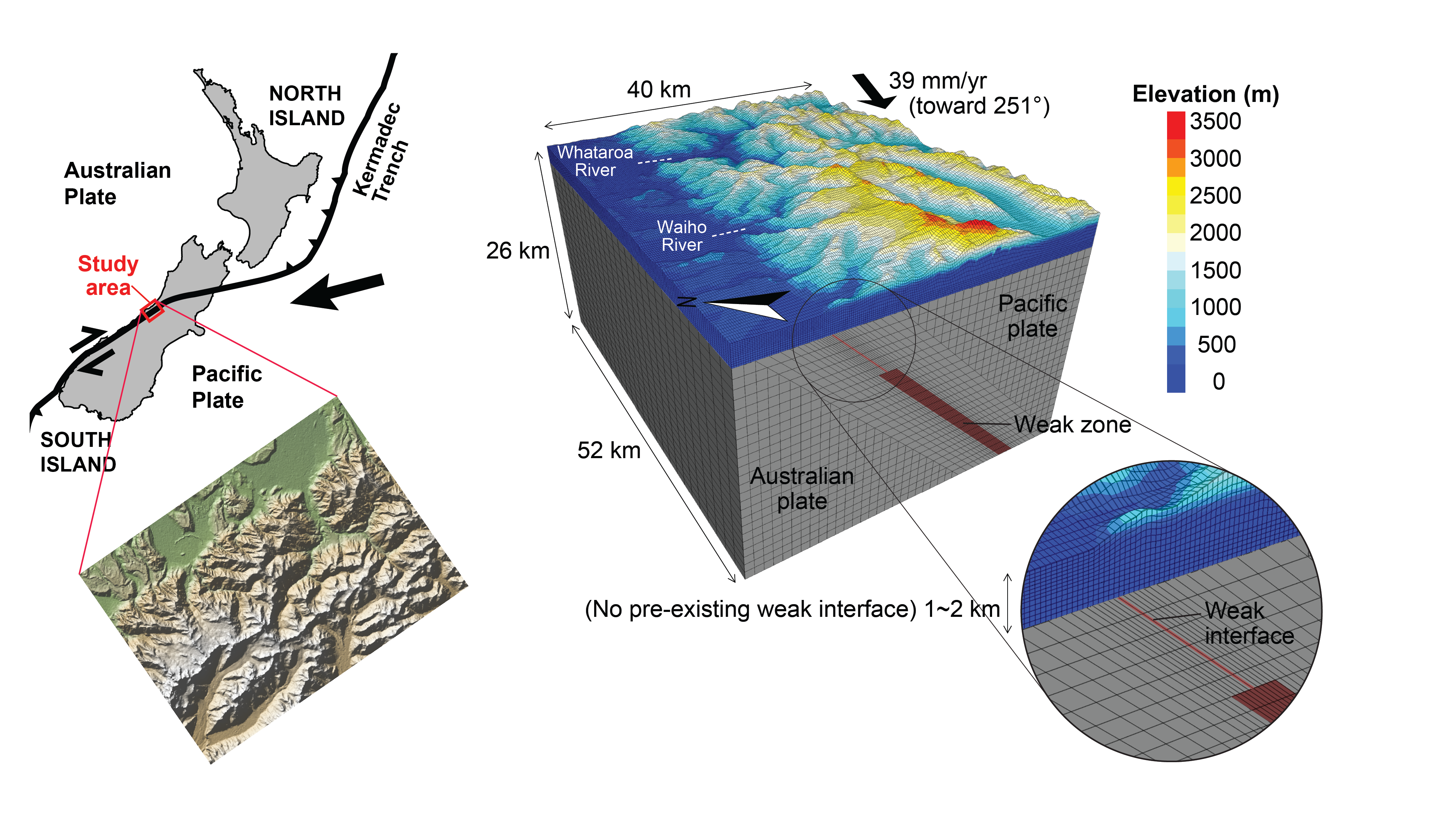
Strain partitioning and fault segmentation in transpressional mountain belts appears linked to stress perturbations controlled by oblique tectonic loading, topographically-induced stress, dynamic stress during fault rupture, and their heterogeneous interactions. Field-based studies alone cannot provide full information on the spatial and temporal variation of stress patterns and the relative impact of the controlling factors due to complexity along with coupling between tectonic deformation and surface processes. For this reason, kinematic and dynamic characteristics of 3-D deformation formed by strain partitioning in an obliquely convergent region such as the Southern Alps, New Zealand, is still poorly understood. In this study, we investigate the numerical solution for 3-D deformation to answer the following questions. (1) How sensitive is strain partitioning and fault evolution to rock rheology and boundary conditions? (2) How are the stress and strain distributions around a fault zone reflected in fault segmentation and how do they relate to the topography?
Model setup
Strain-softening in FLAC3D
The Mohr-Coulomb plastic model in FLAC3D allows simulating strain-hardening/softening behaviors (Itasca, 2012). This can be controlled by yielding parameters such as friction angle, cohesion, dilation angle, and tensile strength, which are a function of plastic strain. In the model, we set up a softening behavior to reduce internal friction angle, cohesion, and tensile strength when/where strain is higher than 0.03.
| Shear strain increment | Fault segments defined as friction angles (blue: fault, red: bedrock) |
|---|---|
Faults initiate from short segmentation, grow as echelon arrays, and become a localized fault zone by the segment linkage.
Strain partitioning sensitivity analysis using direction of the plate displacement and rock strength difference between the weak zone (ϕft) and the stronger surroundings (ϕbedrock)
The relative motion of two plates are generally oblique. To analyze linkage between obliquity and strain partitioning controlled by topography, we performed sensitivity tests using orthogonal (0°), oblique (45°), and highly oblique (74°, obliquity of Alpine fault) motions. To explore the influence of topographic relief on strain partitioning and fault evolution, we also did the sensitivity test using different rock strength.
The obliquity of plate convergence increases from A to C. Greater magnitude of strain partitioning occurs within highly oblique models while strain is localized along discrete shear bands in orthogonal models. Note that even in orthogonal models, river valleys produce complex strain patterns. For a given convergence obliquity, the degree of strain partitioning is a function of the internal friction angle of fault.
Citations
Itasca, 2012. FLAC3D (Fast Lagrangian Analysis of Continua in 3 Dimensions) Version 5.01 Constitutive Models, Itasca Consulting Group Inc. Minneapolis, Minnesota.